Next: Principle of Equal A Up: Statistical Mechanics Previous: Statistical Mechanics
 , and momentum,
, and momentum,  .
In fact, if we know
.
In fact, if we know  and
and  then
we can calculate the state of the system at all subsequent times using the
equation of motion.
In practice, it is impossible to specify
then
we can calculate the state of the system at all subsequent times using the
equation of motion.
In practice, it is impossible to specify
 and
and  exactly, because there is always an intrinsic error in any experimental
measurement.
exactly, because there is always an intrinsic error in any experimental
measurement.
Consider the time evolution of  and
and  .
This can be visualized by plotting
the point (
.
This can be visualized by plotting
the point ( ,
,  ) in the
) in the
 -
- plane. This plane is generally known as phase-space. In general, as time progresses,
the point (
plane. This plane is generally known as phase-space. In general, as time progresses,
the point ( ,
,  ) will trace out some very complicated pattern in
phase-space.
Suppose that we divide phase-space into rectangular cells of uniform dimensions
) will trace out some very complicated pattern in
phase-space.
Suppose that we divide phase-space into rectangular cells of uniform dimensions
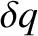 and
and  .
Here,
.
Here, 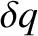 is the intrinsic error in the position measurement, and
is the intrinsic error in the position measurement, and
 the intrinsic error in the momentum measurement. The area of each cell
is
the intrinsic error in the momentum measurement. The area of each cell
is
 |
(5.288) |
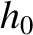 is a small constant having the dimensions of angular momentum.
The coordinates
is a small constant having the dimensions of angular momentum.
The coordinates  and
and  can now be
conveniently specified by indicating
the cell in phase-space into which they plot at any given time.
This procedure automatically ensures that we do not attempt to specify
can now be
conveniently specified by indicating
the cell in phase-space into which they plot at any given time.
This procedure automatically ensures that we do not attempt to specify
 and
and  to an accuracy greater than our experimental error, which would
clearly be pointless.
to an accuracy greater than our experimental error, which would
clearly be pointless.
Let us now consider a single spinless particle moving in three dimensions. In order
to specify the state of the system, we now need to know three  -
- pairs;
that is,
pairs;
that is, 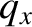 -
-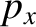 ,
, 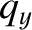 -
-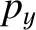 , and
, and 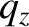 -
-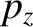 . Incidentally,
the number of
. Incidentally,
the number of  -
- pairs needed to specify the state of the
system is usually called the number of degrees of freedom of the
system. Thus, a single particle moving in one dimension constitutes a one
degree of freedom system, whereas a single particle moving
in three dimensions constitutes a three degree of freedom system.
pairs needed to specify the state of the
system is usually called the number of degrees of freedom of the
system. Thus, a single particle moving in one dimension constitutes a one
degree of freedom system, whereas a single particle moving
in three dimensions constitutes a three degree of freedom system.
Consider the time evolution of 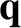 and
and  , where
, where
 , et cetera.
This can be visualized by plotting
the point (
, et cetera.
This can be visualized by plotting
the point (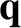 ,
,  ) in the six-dimensional
) in the six-dimensional
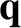 -
- phase-space.
Suppose that we divide the
phase-space.
Suppose that we divide the 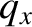 -
-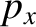 plane
into rectangular cells of uniform dimensions
plane
into rectangular cells of uniform dimensions
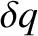 and
and  , and do likewise for the
, and do likewise for the 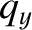 -
-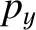 and
and
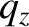 -
-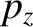 planes. Here,
planes. Here, 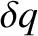 and
and  are again the intrinsic
errors in our measurements of position and momentum, respectively.
This is equivalent to dividing phase-space up into
regular six-dimensional cells of volume
are again the intrinsic
errors in our measurements of position and momentum, respectively.
This is equivalent to dividing phase-space up into
regular six-dimensional cells of volume  .
The coordinates
.
The coordinates 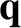 and
and  can now be
conveniently specified by indicating
the cell in phase-space into which they plot at any given time.
Again, this procedure automatically ensures that we do not attempt to specify
can now be
conveniently specified by indicating
the cell in phase-space into which they plot at any given time.
Again, this procedure automatically ensures that we do not attempt to specify
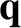 and
and  to an accuracy greater than our experimental error.
to an accuracy greater than our experimental error.
Finally, let us consider a system consisting of  spinless particles moving
classically in three dimensions.
In order to specify
the state of the system, we need to specify a large number of
spinless particles moving
classically in three dimensions.
In order to specify
the state of the system, we need to specify a large number of  -
- pairs.
The requisite
number is simply the number of degrees of freedom,
pairs.
The requisite
number is simply the number of degrees of freedom, 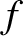 .
For
the present case,
.
For
the present case,
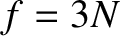 , because each particle needs three
, because each particle needs three  -
- pairs. Thus, phase-space (i.e., the space of all the
pairs. Thus, phase-space (i.e., the space of all the  -
- pairs)
now possesses
pairs)
now possesses 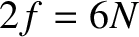 dimensions.
Consider a particular pair of phase-space coordinates,
dimensions.
Consider a particular pair of phase-space coordinates,  and
and
 .
As before, we divide the
.
As before, we divide the  -
- plane into rectangular cells of uniform dimensions
plane into rectangular cells of uniform dimensions
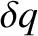 and
and  .
This is equivalent to dividing phase-space into regular
.
This is equivalent to dividing phase-space into regular  dimensional cells of volume
dimensional cells of volume  . The state of the
system is specified by indicating which cell it occupies in phase-space
at any given time.
. The state of the
system is specified by indicating which cell it occupies in phase-space
at any given time.
In principle, we can specify the state of the system to arbitrary
accuracy, by taking the limit
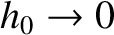 . In reality, we know from
Heisenberg's uncertainty principle (see Section 4.2.7) that it is impossible to simultaneously
measure a coordinate,
. In reality, we know from
Heisenberg's uncertainty principle (see Section 4.2.7) that it is impossible to simultaneously
measure a coordinate,  , and
its associated momentum,
, and
its associated momentum,  , to greater accuracy than
, to greater accuracy than
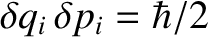 . Here,
. Here,  is Planck's constant divided by
is Planck's constant divided by 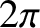 .
This implies that
.
This implies that
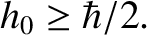 |
(5.289) |
In quantum mechanics, we can specify the state of
the system by giving its wavefunction at time  ,
,
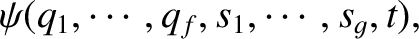 |
(5.290) |
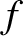 is the number of translational degrees of freedom,
and
is the number of translational degrees of freedom,
and 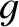 the number of internal (e.g., spin)
degrees of freedom. For instance, if the system
consists of
the number of internal (e.g., spin)
degrees of freedom. For instance, if the system
consists of  spin-one-half particles then there will be
spin-one-half particles then there will be 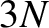 translational
degrees of freedom, and
translational
degrees of freedom, and
 spin degrees of freedom
(because the spin of each particle can either be directed up or down along the
spin degrees of freedom
(because the spin of each particle can either be directed up or down along the
 -axis). Alternatively, if the system is in a stationary
state (see Section 4.2.9) then we can just
specify
-axis). Alternatively, if the system is in a stationary
state (see Section 4.2.9) then we can just
specify 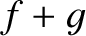 quantum numbers. Either way, the future
time evolution of the wavefunction
is fully determined by Schrödinger's equation.
In reality, this approach is not practical because Schrödinger's equation for the system is
only
known approximately. Typically, we are dealing with a system consisting of many
weakly-interacting particles. We usually know Schrödinger's equation for completely
non-interacting particles, but the component of the equation associated
with particle interactions is either impossibly complicated, or not very well
known. We can define approximate stationary eigenstates
using the Schrödinger's equation for non-interacting particles. The state of the system is
then specified by the quantum numbers identifying these eigenstates. In the absence
of particle interactions, if the system starts off
in a stationary state then it
stays in that state for ever, so its quantum numbers never change. The interactions
allow the system to make transitions between different “stationary”
states, causing its quantum numbers to change in time.
quantum numbers. Either way, the future
time evolution of the wavefunction
is fully determined by Schrödinger's equation.
In reality, this approach is not practical because Schrödinger's equation for the system is
only
known approximately. Typically, we are dealing with a system consisting of many
weakly-interacting particles. We usually know Schrödinger's equation for completely
non-interacting particles, but the component of the equation associated
with particle interactions is either impossibly complicated, or not very well
known. We can define approximate stationary eigenstates
using the Schrödinger's equation for non-interacting particles. The state of the system is
then specified by the quantum numbers identifying these eigenstates. In the absence
of particle interactions, if the system starts off
in a stationary state then it
stays in that state for ever, so its quantum numbers never change. The interactions
allow the system to make transitions between different “stationary”
states, causing its quantum numbers to change in time.