Next: Binomial Probability Distribution Up: Probability Theory Previous: Probability Theory
 . Suppose that a measurement of a given property of
this system can result in a number of distinct outcomes. If we wish to determine the
probability of obtaining a given outcome at an arbitrary time then we can take one of two approaches.
First, we can observe system
. Suppose that a measurement of a given property of
this system can result in a number of distinct outcomes. If we wish to determine the
probability of obtaining a given outcome at an arbitrary time then we can take one of two approaches.
First, we can observe system  at many distinct times; this approach is known as a
time average. Second, we can observe many systems that are identical to
at many distinct times; this approach is known as a
time average. Second, we can observe many systems that are identical to  at an arbitrary time;
this approach is known as an ensemble average. An ensemble average is the most convenient theoretical approach,
and the one that we shall adopt in the following discussion,
whereas a time average is more directly related to real experiments.
at an arbitrary time;
this approach is known as an ensemble average. An ensemble average is the most convenient theoretical approach,
and the one that we shall adopt in the following discussion,
whereas a time average is more directly related to real experiments.
Suppose that there are  systems in our ensemble (i.e., collection of identical systems) and that
systems in our ensemble (i.e., collection of identical systems) and that
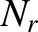 of these systems exhibit the outcome
of these systems exhibit the outcome  . The probability of occurrence of outcome
. The probability of occurrence of outcome  is
defined
is
defined
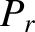 is a number that lies between 0 and 1. If
is a number that lies between 0 and 1. If 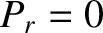 then no systems in the ensemble
exhibit the outcome
then no systems in the ensemble
exhibit the outcome  , even in the limit that the number of systems tends to infinity. This is another way
of saying that outcome
, even in the limit that the number of systems tends to infinity. This is another way
of saying that outcome  is impossible. If
is impossible. If 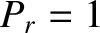 then all systems in the ensemble exhibit the outcome
then all systems in the ensemble exhibit the outcome  ,
even in the limit that the number of systems tends to infinity. This is another way of saying that outcome
,
even in the limit that the number of systems tends to infinity. This is another way of saying that outcome  is certain to occur.
is certain to occur.
Suppose that a measurement of a given property of some physical system  can lead to any one of
can lead to any one of
 mutually exclusive outcomes. Let the total number of systems in the ensemble be
mutually exclusive outcomes. Let the total number of systems in the ensemble be  , and
let the number of systems that exhibit the outcome
, and
let the number of systems that exhibit the outcome  be
be 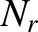 . It follows that
. It follows that
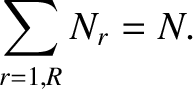 |
(5.2) |
 , and then take the limit that
, and then take the limit that
 , then we obtain the so-called normalization condition,
where use has been made of Equation (5.1). The normalization condition states that the sum of the probabilities of all
of the possible outcomes of a measurement of a given property of system
, then we obtain the so-called normalization condition,
where use has been made of Equation (5.1). The normalization condition states that the sum of the probabilities of all
of the possible outcomes of a measurement of a given property of system  is unity. This condition is equivalent to the self-evident proposition that a measurement of the property is bound to result in one of the possible outcomes of this measurement.
is unity. This condition is equivalent to the self-evident proposition that a measurement of the property is bound to result in one of the possible outcomes of this measurement.
Let us determine the probability of occurrence of outcome  or outcome
or outcome 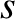 when an observation is made of our
system. Here,
when an observation is made of our
system. Here,  and
and 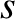 are distinct outcomes. There are
are distinct outcomes. There are  systems in our ensemble that
exhibit either the outcome
systems in our ensemble that
exhibit either the outcome  or the outcome
or the outcome 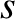 , so
, so
 or the outcome
or the outcome 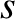 is the sum of the probabilities of occurrence of these two outcomes.
For example, the probability
of throwing a
is the sum of the probabilities of occurrence of these two outcomes.
For example, the probability
of throwing a  on a six-sided die is
on a six-sided die is 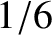 . Likewise, the probability of throwing a 2 is
. Likewise, the probability of throwing a 2 is 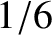 . Hence, the
probability of throwing a
. Hence, the
probability of throwing a  or a
or a 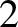 is
is
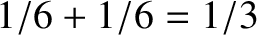 . The previous result can easily be extended to deal
with more that two alternative outcomes.
. The previous result can easily be extended to deal
with more that two alternative outcomes.
Suppose that our system can exhibit two different types of outcome. Type-1 outcomes are labeled
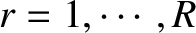 .
Type-2 outcomes are labeled
.
Type-2 outcomes are labeled
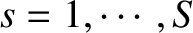 . Let there be
. Let there be  systems in our ensemble, and let
systems in our ensemble, and let 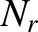 of them
exhibit the type-1 outcome
of them
exhibit the type-1 outcome  , and let
, and let  of them exhibit the type-2 outcome
of them exhibit the type-2 outcome 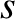 . The probability of outcome
. The probability of outcome 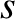 is
is
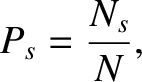 |
(5.5) |
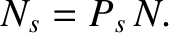 |
(5.6) |
 is taken as read; see Equation (5.1).] By analogy, the number of systems that
exhibit the type-1 outcome
is taken as read; see Equation (5.1).] By analogy, the number of systems that
exhibit the type-1 outcome  and the type-2 outcome
and the type-2 outcome 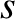 is
is
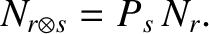 |
(5.7) |
 and the type-2 outcome
and the type-2 outcome 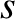 simultaneously is
where use has been made of Equation (5.1). However, the previous result is only valid provided outcomes
simultaneously is
where use has been made of Equation (5.1). However, the previous result is only valid provided outcomes
 and
and 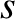 are statistically independent of one another. In other words, obtaining the outcome
are statistically independent of one another. In other words, obtaining the outcome  must
not affect the probability of obtaining the outcome
must
not affect the probability of obtaining the outcome 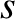 . As an example of the previous result, consider a
system consisting of two six-sided dies. The probability of throwing a 1 on either die is
. As an example of the previous result, consider a
system consisting of two six-sided dies. The probability of throwing a 1 on either die is 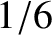 . Hence, the probability
of simultaneously throwing a 1 on both dies is
. Hence, the probability
of simultaneously throwing a 1 on both dies is
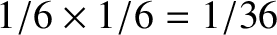 . The previous result can easily be extended to
deal with more than two types of outcome.
. The previous result can easily be extended to
deal with more than two types of outcome.