Next: Mean, Variance, and Standard Up: Probability Theory Previous: Probability
 and
and 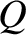 , and
let
, and
let  and
and  be the respective probabilities of these outcomes. It follows from Equation (5.3) that
be the respective probabilities of these outcomes. It follows from Equation (5.3) that
Consider an ensemble of  two-outcome systems like the one just discussed.
Let
two-outcome systems like the one just discussed.
Let  be the number of systems in the ensemble that exhibit outcome
be the number of systems in the ensemble that exhibit outcome  , and let
, and let 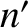 be the
number of systems that exhibit outcome
be the
number of systems that exhibit outcome 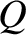 . It is evident that
. It is evident that
Let us determine the probability,  , that
, that  systems in our ensemble exhibit outcome
systems in our ensemble exhibit outcome  .
Making use of a straightforward extension of Equation (5.8), the probability that
.
Making use of a straightforward extension of Equation (5.8), the probability that  systems in the ensemble exhibit outcome
systems in the ensemble exhibit outcome
 , and that
, and that 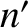 exhibit outcome
exhibit outcome 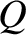 , is
, is
 systems in the ensemble exhibit the outcome
systems in the ensemble exhibit the outcome  can
be achieved in many alternative ways. Let
can
be achieved in many alternative ways. Let 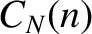 be the number of distinct configurations of
be the number of distinct configurations of  systems by which
systems by which  of these systems exhibit outcome
of these systems exhibit outcome  . Making use of a straightforward extension of Equation (5.4), as well as Equations (5.10) and
(5.11), we deduce that
. Making use of a straightforward extension of Equation (5.4), as well as Equations (5.10) and
(5.11), we deduce that
Consider  systems exhibiting the outcome
systems exhibiting the outcome  . The number of ways that these systems can
be distributed between
. The number of ways that these systems can
be distributed between  systems is
systems is
![$\displaystyle N\,(N-1)\,(N-2)\cdots [N-(n-1)] = \frac{N!}{(N-n)!}.$](img3396.png) |
(5.13) |
 systems to exhibit the first outcome
systems to exhibit the first outcome  , then we can
choose any one of the remaining
, then we can
choose any one of the remaining  systems to exhibit the second outcome
systems to exhibit the second outcome  , and so on.
However, some of the
, and so on.
However, some of the 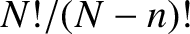 distributions will just be permutations of the systems exhibiting outcome
distributions will just be permutations of the systems exhibiting outcome
 among themselves. Such permutations do not correspond to distinct distributions. Now, the
number of permutations of
among themselves. Such permutations do not correspond to distinct distributions. Now, the
number of permutations of  quantities among
quantities among  places is
places is 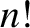 . Hence, we deduce that
. Hence, we deduce that
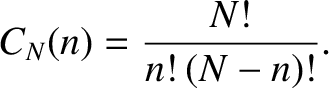 |
(5.14) |
The well-known algebraic expansion of a binomial of the form  is
is
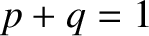 , which implies that
, which implies that  . Thus, the previous two equations
yield
. Thus, the previous two equations
yield
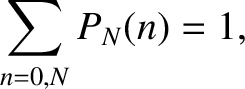 |
(5.17) |
Suppose that outcomes  and
and  represent steps to the right and steps to the left taken by a drunken
man. The net number of steps to the right taken is
represent steps to the right and steps to the left taken by a drunken
man. The net number of steps to the right taken is
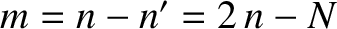 , where use has been made of Equation (5.10). Thus,
, where use has been made of Equation (5.10). Thus,
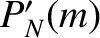 , that
, that  assumes a certain value after
assumes a certain value after  steps is equal to
the probability that
steps is equal to
the probability that  assumes the value
assumes the value 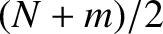 . In other words,
. In other words,
Suppose, finally, that some physical system  can exhibit many possible outcomes,
can exhibit many possible outcomes,  ,
, 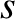 ,
,  , et cetera. If
we are only interested in outcome
, et cetera. If
we are only interested in outcome  then we could label all of the other outcomes `not
then we could label all of the other outcomes `not  ' or
' or  .
In this case, we have recovered a system to which the binomial probability distribution applies.
.
In this case, we have recovered a system to which the binomial probability distribution applies.