Next: Application to Binomial Probability Up: Probability Theory Previous: Binomial Probability Distribution
 . Suppose that a measurement of a particular physical property of this
system,
. Suppose that a measurement of a particular physical property of this
system,  , can result in one of
, can result in one of  distinct outcomes. Let outcome
distinct outcomes. Let outcome  be associated with
be associated with  taking the value
taking the value 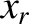 . Consider an ensemble of
. Consider an ensemble of  systems that are identical to system
systems that are identical to system  . Let
. Let 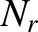 be the number of systems in the ensemble that exhibit the outcome
be the number of systems in the ensemble that exhibit the outcome  . The mean value of
. The mean value of  is, by definition, the average of a very large number of measurements of
is, by definition, the average of a very large number of measurements of  . In other words,
. In other words,
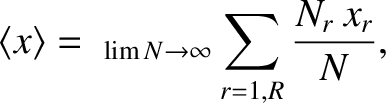 |
(5.20) |
Let
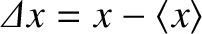 |
(5.22) |
 from the mean value. Obviously,
from the mean value. Obviously,
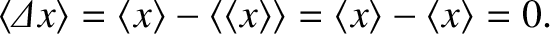 |
(5.23) |
Consider
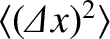 . This quantity, which is known as the variance of
. This quantity, which is known as the variance of  , is positive definite.
It can only take the value 0 if all measurement of
, is positive definite.
It can only take the value 0 if all measurement of  result in the mean value. Thus, the variance of
result in the mean value. Thus, the variance of  measures the degree of scatter about the mean value.
It follows that
measures the degree of scatter about the mean value.
It follows that
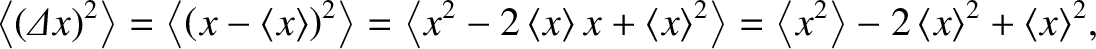 |
(5.24) |
Finally, the quantity
is known as the standard deviation of .
The
standard deviation is essentially the width of the range of probable values over which
.
The
standard deviation is essentially the width of the range of probable values over which
 is distributed around its mean value,
is distributed around its mean value,
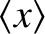 .
.