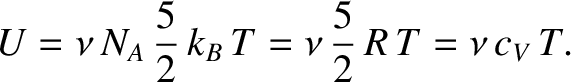Internal Energy
Consider a monatomic gas such as helium. An individual helium atom can only store energy in its translational
motion. As we saw in Section 5.3.4, the mean energy associated with this motion is
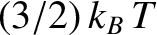 . Hence, the
internal energy of a gas consisting of
. Hence, the
internal energy of a gas consisting of 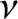 moles of helium atoms is
moles of helium atoms is
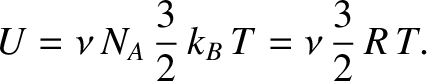 |
(5.188) |
However, according to Equation (5.108),
 |
(5.189) |
where  is the molar specific heat capacity of the gas at constant volume. The previous two equations
imply that the molar specific heat capacity of a helium gas (or any monatomic gas) is
is the molar specific heat capacity of the gas at constant volume. The previous two equations
imply that the molar specific heat capacity of a helium gas (or any monatomic gas) is
 |
(5.190) |
in accordance with Equation (5.106).
Consider a diatomic gas such as hydrogen. An individual hydrogen molecule can store energy in its
translational motion, but can also store energy in its rotational motion.
In principle, a molecule has three principal axes of rotation about which it could rotate. (See Sections 1.7.2 and 1.7.3.) Hence, the net rotational kinetic energy is
 |
(5.191) |
where  is the angular momentum about the
is the angular momentum about the  -axis,
-axis, 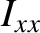 is the principal moment of inertia for rotation about the
is the principal moment of inertia for rotation about the  -axis, et cetera. Note that the previous expression consists of three terms that are quadratic in a
momentum component. Hence, according to the law of equipartition of energy, the mean rotational energy
of the molecule should be
-axis, et cetera. Note that the previous expression consists of three terms that are quadratic in a
momentum component. Hence, according to the law of equipartition of energy, the mean rotational energy
of the molecule should be
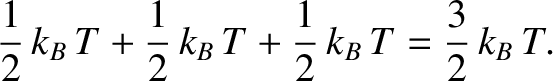 |
(5.192) |
In fact, this is not the case. The reason for the discrepancy is that one of the principal axes of
rotation of a hydrogen molecule corresponds to the axis that passes through the nuclei of the two hydrogen atoms that constitute the molecule.
The principal moment of inertia for rotation about this axis is much smaller than the principal
moments of inertia for rotation about the other two principal axes. In fact, the former moment
of inertia is of order
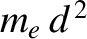 , where
, where 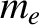 is the mass of an electron, and
is the mass of an electron, and 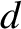 the radius
of a hydrogen atom (the contribution of the protons to the moment is negligible), whereas the latter two moments of inertia are of order
the radius
of a hydrogen atom (the contribution of the protons to the moment is negligible), whereas the latter two moments of inertia are of order
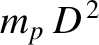 , where
, where 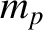 is the
mass of a proton, and
is the
mass of a proton, and 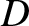 the length of the atomic bond joining the two hydrogen atoms. Given that
the length of the atomic bond joining the two hydrogen atoms. Given that
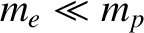 , while
, while 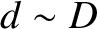 , the former moment of
inertia is indeed much smaller than the latter two. It turns out that quantum mechanical considerations
prevent a degree of rotational freedom with an anomalously small moment of inertia from
contributing
, the former moment of
inertia is indeed much smaller than the latter two. It turns out that quantum mechanical considerations
prevent a degree of rotational freedom with an anomalously small moment of inertia from
contributing
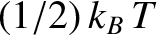 to the mean energy of the molecule. (See Section 5.5.8.) Hence, the mean rotational energy
of a hydrogen molecule (or any diatomic molecule) is
to the mean energy of the molecule. (See Section 5.5.8.) Hence, the mean rotational energy
of a hydrogen molecule (or any diatomic molecule) is
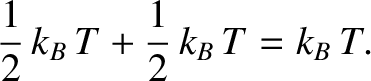 |
(5.193) |
According to the previous discussion, the mean energy of a hydrogen molecule is
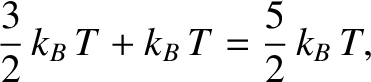 |
(5.194) |
where the former contribution is the molecule's mean translation kinetic energy, whereas the latter contribution
is the molecule's mean rotational kinetic energy. Hence, the
internal energy of a gas consisting of 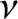 moles of hydrogen molecules is [see Equation (5.189)]
moles of hydrogen molecules is [see Equation (5.189)]
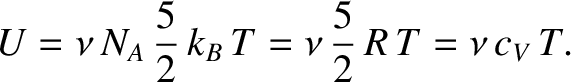 |
(5.195) |
It follows that the molar specific heat capacity at constant volume of a hydrogen gas (or any diatomic gas) is
 |
(5.196) |
in accordance with Equation (5.107).
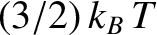 . Hence, the
internal energy of a gas consisting of
. Hence, the
internal energy of a gas consisting of 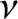 moles of helium atoms is
moles of helium atoms is
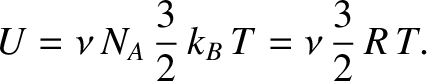
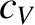 is the molar specific heat capacity of the gas at constant volume. The previous two equations
imply that the molar specific heat capacity of a helium gas (or any monatomic gas) is
is the molar specific heat capacity of the gas at constant volume. The previous two equations
imply that the molar specific heat capacity of a helium gas (or any monatomic gas) is

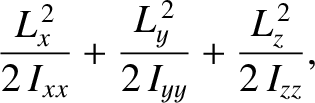
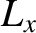 is the angular momentum about the
is the angular momentum about the  -axis,
-axis, 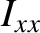 is the principal moment of inertia for rotation about the
is the principal moment of inertia for rotation about the  -axis, et cetera. Note that the previous expression consists of three terms that are quadratic in a
momentum component. Hence, according to the law of equipartition of energy, the mean rotational energy
of the molecule should be
-axis, et cetera. Note that the previous expression consists of three terms that are quadratic in a
momentum component. Hence, according to the law of equipartition of energy, the mean rotational energy
of the molecule should be
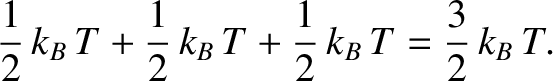
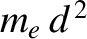 , where
, where 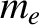 is the mass of an electron, and
is the mass of an electron, and 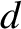 the radius
of a hydrogen atom (the contribution of the protons to the moment is negligible), whereas the latter two moments of inertia are of order
the radius
of a hydrogen atom (the contribution of the protons to the moment is negligible), whereas the latter two moments of inertia are of order
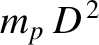 , where
, where 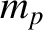 is the
mass of a proton, and
is the
mass of a proton, and 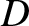 the length of the atomic bond joining the two hydrogen atoms. Given that
the length of the atomic bond joining the two hydrogen atoms. Given that
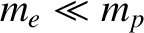 , while
, while 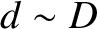 , the former moment of
inertia is indeed much smaller than the latter two. It turns out that quantum mechanical considerations
prevent a degree of rotational freedom with an anomalously small moment of inertia from
contributing
, the former moment of
inertia is indeed much smaller than the latter two. It turns out that quantum mechanical considerations
prevent a degree of rotational freedom with an anomalously small moment of inertia from
contributing
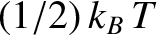 to the mean energy of the molecule. (See Section 5.5.8.) Hence, the mean rotational energy
of a hydrogen molecule (or any diatomic molecule) is
to the mean energy of the molecule. (See Section 5.5.8.) Hence, the mean rotational energy
of a hydrogen molecule (or any diatomic molecule) is
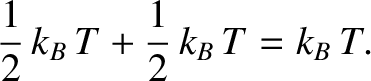
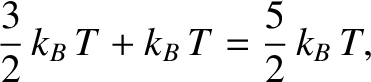
 moles of hydrogen molecules is [see Equation (5.189)]
moles of hydrogen molecules is [see Equation (5.189)]