Next: Maxwell Velocity Distribution Up: Applications of Statistical Mechanics Previous: Specific Heat Capacties
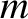 and momentum
and momentum
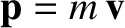 then its kinetic energy of translation is
The kinetic energy of other molecules does not involve the momentum,
then its kinetic energy of translation is
The kinetic energy of other molecules does not involve the momentum, 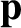 ,
of this particular molecule.
Moreover, the potential energy of interaction between molecules
depends only on their position coordinates, and is, thus, independent of
,
of this particular molecule.
Moreover, the potential energy of interaction between molecules
depends only on their position coordinates, and is, thus, independent of
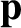 . Any internal rotational, vibrational, electronic, or nuclear degrees
of freedom of the molecule also do not involve
. Any internal rotational, vibrational, electronic, or nuclear degrees
of freedom of the molecule also do not involve 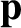 . Hence, the essential
conditions of the equipartition theorem are satisfied. (At least, in the classical
approximation.) Because Equation (5.400) contains three independent
quadratic terms, there
are clearly three degrees of freedom associated with translation (one for each
dimension of space), so the translational contribution to the molar heat capacity
of gases is
. Hence, the essential
conditions of the equipartition theorem are satisfied. (At least, in the classical
approximation.) Because Equation (5.400) contains three independent
quadratic terms, there
are clearly three degrees of freedom associated with translation (one for each
dimension of space), so the translational contribution to the molar heat capacity
of gases is
Suppose that our gas is contained in a cubic enclosure of dimensions 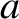 . According
to Schrödinger's equation, the quantized translational
energy levels of an individual molecule are given by
. According
to Schrödinger's equation, the quantized translational
energy levels of an individual molecule are given by
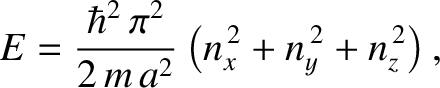 |
(5.402) |
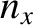 ,
, 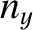 , and
, and 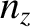 are positive-integer quantum numbers. (See Section 4.4.2.) Clearly, the
spacing between the energy levels can be made arbitrarily small by increasing the
size of the enclosure. This implies that translational degrees of freedom can
be treated classically, so that
Equation (5.401) is always valid. (Except very close to absolute zero.)
We conclude that all
gases possess a minimum molar heat capacity of
are positive-integer quantum numbers. (See Section 4.4.2.) Clearly, the
spacing between the energy levels can be made arbitrarily small by increasing the
size of the enclosure. This implies that translational degrees of freedom can
be treated classically, so that
Equation (5.401) is always valid. (Except very close to absolute zero.)
We conclude that all
gases possess a minimum molar heat capacity of 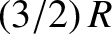 due to the
translational degrees of freedom of their constituent molecules.
due to the
translational degrees of freedom of their constituent molecules.
The electronic degrees of freedom of gas molecules (i.e., the possible
configurations of electrons orbiting the atomic nuclei) typically give rise
to absorption and emission in the
ultraviolet or visible regions of the spectrum. It follows from Table 5.1 that
electronic degrees of freedom are frozen out at room temperature. Similarly,
nuclear degrees of freedom (i.e., the possible configurations of protons
and neutrons in the atomic nuclei) are frozen out because they are associated
with absorption and emission in the X-ray and 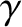 -ray regions of the
electromagnetic spectrum. In fact, the only additional degrees of freedom
that we need worry about for gases are rotational and vibrational degrees of freedom.
These typically give rise to absorption lines in the infrared region of the
spectrum.
-ray regions of the
electromagnetic spectrum. In fact, the only additional degrees of freedom
that we need worry about for gases are rotational and vibrational degrees of freedom.
These typically give rise to absorption lines in the infrared region of the
spectrum.
The rotational kinetic energy of a molecule tumbling in space can be written
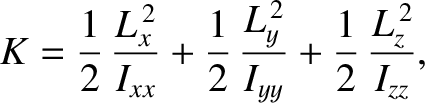 |
(5.403) |
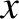 -,
-, 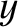 -, and
-, and 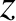 -axes are the so called principal axes of rotation
of the molecule (these are mutually perpendicular),
-axes are the so called principal axes of rotation
of the molecule (these are mutually perpendicular), 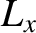 ,
, 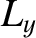 ,
and
,
and 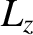 are the angular momenta about these axes, and
are the angular momenta about these axes, and
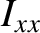 ,
, 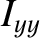 , and
, and 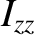 are the principal moments of inertia about these
axes. (See Sections 1.7.2 and 1.7.3.) No other degrees of freedom depend on the angular momenta. Because the kinetic energy of rotation is the sum of three quadratic
terms, the rotational contribution to the molar heat capacity of gases
is
are the principal moments of inertia about these
axes. (See Sections 1.7.2 and 1.7.3.) No other degrees of freedom depend on the angular momenta. Because the kinetic energy of rotation is the sum of three quadratic
terms, the rotational contribution to the molar heat capacity of gases
is
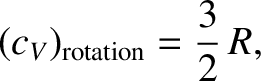 |
(5.404) |
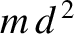 , where
, where 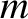 is the molecular mass, and
is the molecular mass, and
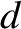 is the typical interatomic spacing in the molecule.
A special case arises if the molecule is linear
(e.g., if the molecule is diatomic). In this case, one of the principal axes lies
along the line of centers of the atoms. The moment of inertia about this axis
is of order
is the typical interatomic spacing in the molecule.
A special case arises if the molecule is linear
(e.g., if the molecule is diatomic). In this case, one of the principal axes lies
along the line of centers of the atoms. The moment of inertia about this axis
is of order
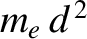 , where
, where 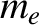 is the electron mass. (See Section 5.3.6.) Because
is the electron mass. (See Section 5.3.6.) Because
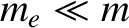 , it follows that the moment of inertia about the line of
centers is minuscule compared to the moments of inertia about the other two
principal axes. In quantum mechanics, angular momentum is quantized in units
of
, it follows that the moment of inertia about the line of
centers is minuscule compared to the moments of inertia about the other two
principal axes. In quantum mechanics, angular momentum is quantized in units
of 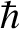 . The energy levels of a rigid rotator spinning about a principal axis are written
. The energy levels of a rigid rotator spinning about a principal axis are written
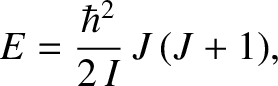 |
(5.405) |
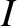 is the moment of inertia, and
is the moment of inertia, and 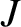 is
a non-negative integer. Note the inverse dependence of the spacing between energy levels
on the moment
of inertia. It is clear that, for the case of a linear molecule, the rotational
degree of freedom associated with spinning along the line of centers of the
atoms is frozen out at room
temperature, given the very small moment of inertia along this axis, and, hence,
the very widely spaced rotational energy levels.
Thus, the rotational contribution to the molar heat capacity of a diatomic gas is
is
a non-negative integer. Note the inverse dependence of the spacing between energy levels
on the moment
of inertia. It is clear that, for the case of a linear molecule, the rotational
degree of freedom associated with spinning along the line of centers of the
atoms is frozen out at room
temperature, given the very small moment of inertia along this axis, and, hence,
the very widely spaced rotational energy levels.
Thus, the rotational contribution to the molar heat capacity of a diatomic gas is
 |
(5.406) |
Classically, the vibrational degrees of freedom of a molecule are studied by
standard normal mode analysis of the
molecular
structure. Each normal mode behaves like an
independent harmonic oscillator, and, therefore,
contributes 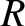 to the molar specific heat of the gas [
to the molar specific heat of the gas [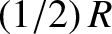 from the
kinetic energy of vibration, and
from the
kinetic energy of vibration, and 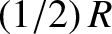 from the potential energy of
vibration]. A molecule containing
from the potential energy of
vibration]. A molecule containing 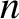 atoms has
atoms has 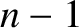 normal modes of vibration.
For instance, a diatomic molecule has just one normal mode (corresponding to
periodic stretching of the bond between the two atoms). Thus, the classical
contribution to the specific heat from vibrational degrees of freedom is
normal modes of vibration.
For instance, a diatomic molecule has just one normal mode (corresponding to
periodic stretching of the bond between the two atoms). Thus, the classical
contribution to the specific heat from vibrational degrees of freedom is
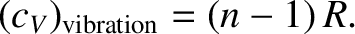 |
(5.407) |
So, do any of the rotational and vibrational degrees of freedom
actually make a contribution to the specific heats of gases at room temperature,
once quantum effects have been taken into consideration? We can answer this
question by
examining just one piece of data. Figure 5.4 shows the
infrared absorption spectrum of hydrogen chloride gas. The absorption lines correspond
to simultaneous transitions between different vibrational and rotational energy
levels. Hence, this is usually called a vibration-rotation spectrum. The missing
line at about 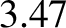 microns corresponds to a pure vibrational transition from the
ground state to the first excited state.
(Pure vibrational transitions are
forbidden; hydrogen chloride molecules always have to simultaneously change their rotational energy level if they are to couple effectively to electromagnetic radiation.)
The longer wavelength absorption lines correspond to vibrational transitions in
which there is a simultaneous decrease in the rotational energy level.
Likewise, the
shorter wavelength absorption lines correspond to vibrational transitions in which
there is a simultaneous increase in the rotational energy level. It is clear that
the rotational energy levels are more closely spaced than the vibrational energy
levels. The pure vibrational transition gives rise to absorption at
about
microns corresponds to a pure vibrational transition from the
ground state to the first excited state.
(Pure vibrational transitions are
forbidden; hydrogen chloride molecules always have to simultaneously change their rotational energy level if they are to couple effectively to electromagnetic radiation.)
The longer wavelength absorption lines correspond to vibrational transitions in
which there is a simultaneous decrease in the rotational energy level.
Likewise, the
shorter wavelength absorption lines correspond to vibrational transitions in which
there is a simultaneous increase in the rotational energy level. It is clear that
the rotational energy levels are more closely spaced than the vibrational energy
levels. The pure vibrational transition gives rise to absorption at
about 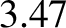 microns, which corresponds to infrared radiation of frequency
microns, which corresponds to infrared radiation of frequency
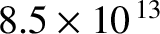 hertz with an associated
radiation “temperature” of 4,100 K. We
conclude that
the vibrational degrees of freedom of hydrogen chloride, or any other small molecule,
are frozen out at room temperature. The rotational transitions split the
vibrational lines by about
hertz with an associated
radiation “temperature” of 4,100 K. We
conclude that
the vibrational degrees of freedom of hydrogen chloride, or any other small molecule,
are frozen out at room temperature. The rotational transitions split the
vibrational lines by about 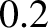 microns. This implies that pure rotational
transitions would be associated with infrared radiation of frequency
microns. This implies that pure rotational
transitions would be associated with infrared radiation of frequency
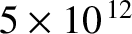 hertz and corresponding
radiation “temperature” 240 K. We
conclude that the rotational degrees of freedom of hydrogen chloride, or any other small
molecule, are not frozen out at room temperature, and probably contribute the
classical
hertz and corresponding
radiation “temperature” 240 K. We
conclude that the rotational degrees of freedom of hydrogen chloride, or any other small
molecule, are not frozen out at room temperature, and probably contribute the
classical 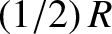 to the molar specific heat. There is one proviso, however.
Linear molecules (like hydrogen chloride) effectively only have two rotational degrees of
freedom (instead of the usual three), because of the very small moment
of inertia of such molecules along the line of centers of the atoms.
to the molar specific heat. There is one proviso, however.
Linear molecules (like hydrogen chloride) effectively only have two rotational degrees of
freedom (instead of the usual three), because of the very small moment
of inertia of such molecules along the line of centers of the atoms.
![\includegraphics[width=0.85\textwidth]{Chapter06/h2.eps}](img4215.png) |
Figure 5.5 shows the variation of the molar heat capacity at constant volume
of gaseous molecular hydrogen (i.e., 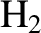 ) with temperature. The expected contribution
from the translational degrees of freedom is
) with temperature. The expected contribution
from the translational degrees of freedom is 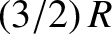 (there are
three translational degrees of freedom per molecule). The
expected contribution at
high temperatures from the rotational degrees of freedom is
(there are
three translational degrees of freedom per molecule). The
expected contribution at
high temperatures from the rotational degrees of freedom is 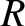 (there are effectively
two rotational degrees of freedom per molecule). Finally, the expected contribution at high temperatures from the vibrational degrees of freedom is
(there are effectively
two rotational degrees of freedom per molecule). Finally, the expected contribution at high temperatures from the vibrational degrees of freedom is 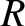 (there
is one vibrational degree of freedom per molecule). It can be seen that,
as the temperature rises, the rotational, and then the vibrational, degrees
of freedom eventually make their full classical contributions to the heat
capacity.
(there
is one vibrational degree of freedom per molecule). It can be seen that,
as the temperature rises, the rotational, and then the vibrational, degrees
of freedom eventually make their full classical contributions to the heat
capacity.