Next: Power Up: Rigid Body Rotation Previous: Moment of Inertia Tensor
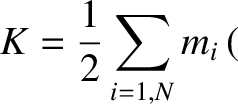 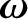 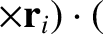 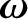 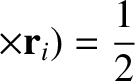 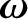 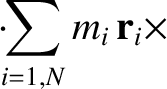 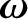 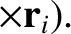 |
(1.194) |
For the special case of an axisymmetric body, making use of Equation (1.190), we obtain
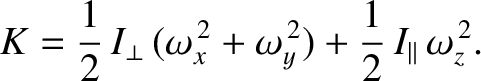 |
(1.196) |
For the special case of a body rotating about a principal axis of rotation,
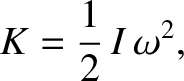 |
(1.197) |
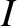 is the associated principal moment of inertia.
More generally,
is the associated principal moment of inertia.
More generally,
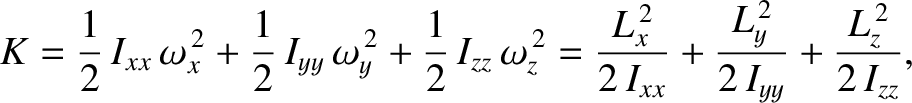 |
(1.198) |