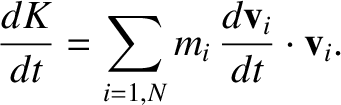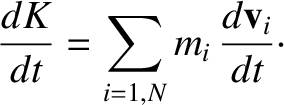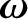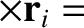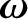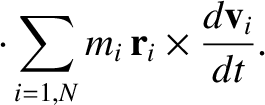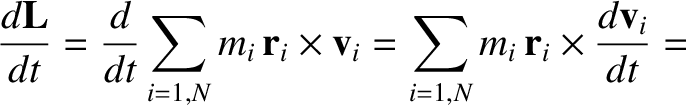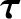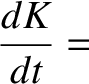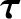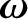Power

It follows from Equation (1.193) that

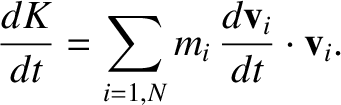$$\frac{dK}{dt} =\sum_{i=1,N}m_i\,\frac{d{\bf v}_i}{dt}\cdot{\bf v}_i.$$ (1.199)

Making use of Equation (1.181), we obtain

$$\frac{dK}{dt} = \sum_{i=1,N} m_i\,\frac{d{\bf v}_i}{dt}\cdot \mbox{\boldmath$\omega$} \times {\bf r}_i = \mbox{\boldmath$\omega$} \cdot\sum_{i=1,N} m_i\,{\bf r}_i\times \frac{d{\bf v}_i}{dt}.$$ (1.200)

However, according to Equations (1.180) and (1.182),

$$\frac{d{\bf L}}{dt} = \frac{d}{dt}\sum_{i=1,N} m_i\,{\bf r}_i\times{\bf v}_i= \sum_{i=1,N} m_i\,{\bf r}_i\times \frac{d{\bf v}_i}{dt}= \mbox{\boldmath$\tau$} .$$ (1.201)

Hence, we obtain

$$\frac{dK}{dt} = \mbox{\boldmath$\tau$} \cdot \mbox{\boldmath$\omega$} .$$ (1.202)

The right-hand side of the previous equation specified the work per unit time done on the system by the external torque.