In 1827, Robert Brown was studying pollen grains of the plant Clarkia pulchella suspended in water under a microscope when he observed minute particles, ejected by the pollen grains, executing a jittery motion. Let us examine this phenomenon, which is known as Brownian motion.
Consider a particle of mass  that is suspended in a fluid.
Let us investigate the motion of this particle parallel to the
that is suspended in a fluid.
Let us investigate the motion of this particle parallel to the  -axis.
The particle is subject to two types of force. First, a set of impulsive forces due to molecular bombardment.
Second, a retarding force that is proportional to the particle's instantaneous speed through the
surrounding fluid. Thus, the particle's equation of motion along the
-axis.
The particle is subject to two types of force. First, a set of impulsive forces due to molecular bombardment.
Second, a retarding force that is proportional to the particle's instantaneous speed through the
surrounding fluid. Thus, the particle's equation of motion along the  -axis can
be written
-axis can
be written
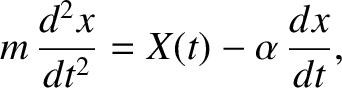 |
(5.197) |
where 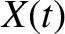 is the impulsive force due to molecular bombardment, and
is the impulsive force due to molecular bombardment, and
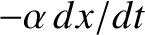 the retarding force.
It follows that
the retarding force.
It follows that
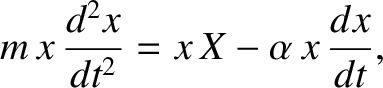 |
(5.198) |
which can also be written
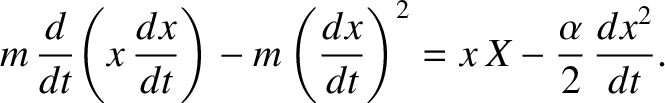 |
(5.199) |
Taking the ensemble average of the previous equation, we obtain
 |
(5.200) |
However,
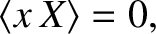 |
(5.201) |
because  and
and  are uncorrelated random variables whose mean values are zero. Furthermore,
are uncorrelated random variables whose mean values are zero. Furthermore,
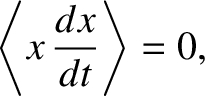 |
(5.202) |
because  and
and  are also uncorrelated random variables whose mean values are zero.
Finally,
are also uncorrelated random variables whose mean values are zero.
Finally,
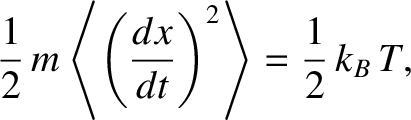 |
(5.203) |
by the law of equipartition of energy, where  is the temperature of the fluid. (See Section 5.3.4.)
It follows from the previous four equations that
is the temperature of the fluid. (See Section 5.3.4.)
It follows from the previous four equations that
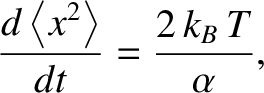 |
(5.204) |
which can be integrated to give
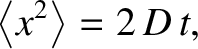 |
(5.205) |
where
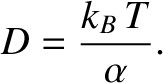 |
(5.206) |
It can be seen, by comparison with the analysis of Sections 5.1.5 and 5.1.7, that molecular bombardment
causes a particle immersed in a fluid to execute a random walk along the  -axis with diffusivity
-axis with diffusivity 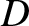 .
.
Suppose that the particle is a sphere of radius 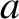 . Furthermore, suppose that the retarding force
acting on the particle is due to fluid viscosity. According to Stokes's law,
. Furthermore, suppose that the retarding force
acting on the particle is due to fluid viscosity. According to Stokes's law,
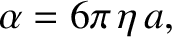 |
(5.207) |
where 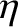 is the viscosity of the fluid. It follows that
is the viscosity of the fluid. It follows that
 |
(5.208) |
This result, which was first obtained by Einstein in 1905, and was verified experimentally by Jean B. Perrin in 1910,
served as the first convincing evidence of the existence of atoms and molecules. Note that the previous diffusivity
scales as the inverse of the particle radius. Hence, only relatively small particles are likely to exhibit noticable
Brownian motion.
 that is suspended in a fluid.
Let us investigate the motion of this particle parallel to the
that is suspended in a fluid.
Let us investigate the motion of this particle parallel to the  -axis.
The particle is subject to two types of force. First, a set of impulsive forces due to molecular bombardment.
Second, a retarding force that is proportional to the particle's instantaneous speed through the
surrounding fluid. Thus, the particle's equation of motion along the
-axis.
The particle is subject to two types of force. First, a set of impulsive forces due to molecular bombardment.
Second, a retarding force that is proportional to the particle's instantaneous speed through the
surrounding fluid. Thus, the particle's equation of motion along the  -axis can
be written
-axis can
be written
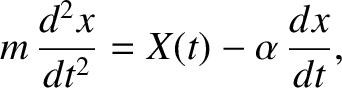
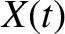 is the impulsive force due to molecular bombardment, and
is the impulsive force due to molecular bombardment, and
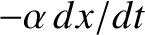 the retarding force.
It follows that
the retarding force.
It follows that
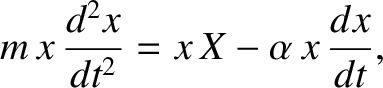
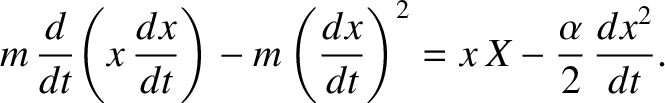

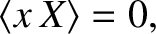
 and
and  are uncorrelated random variables whose mean values are zero. Furthermore,
are uncorrelated random variables whose mean values are zero. Furthermore,
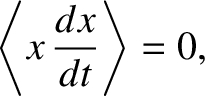
 and
and  are also uncorrelated random variables whose mean values are zero.
Finally,
are also uncorrelated random variables whose mean values are zero.
Finally,
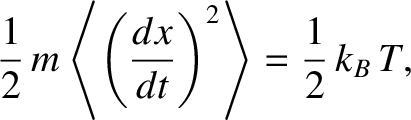
 is the temperature of the fluid. (See Section 5.3.4.)
It follows from the previous four equations that
is the temperature of the fluid. (See Section 5.3.4.)
It follows from the previous four equations that
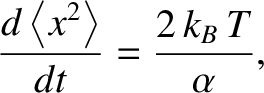
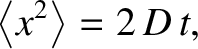
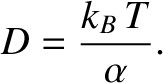
 -axis with diffusivity
-axis with diffusivity 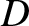 .
.
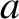 . Furthermore, suppose that the retarding force
acting on the particle is due to fluid viscosity. According to Stokes's law,
. Furthermore, suppose that the retarding force
acting on the particle is due to fluid viscosity. According to Stokes's law,
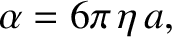
 is the viscosity of the fluid. It follows that
is the viscosity of the fluid. It follows that
