Random Walk
The so-called random walk is a stochastic process that governs, for example, the path traced by a molecule as it travels through a liquid or a gas, while constantly colliding with the other molecules in the medium.
(See Section 5.3.9.)
Consider a random walk in one dimension. Suppose that a molecule takes steps of
equal length  along the
along the  -axis. Suppose, further, that the steps are taken to the left (i.e., in the negative
-axis. Suppose, further, that the steps are taken to the left (i.e., in the negative
 -direction) or to the
right, at random, with equal probabilities. Let
-direction) or to the
right, at random, with equal probabilities. Let 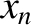 be the molecule's
be the molecule's  coordinate after
coordinate after  steps. It is assumed that
steps. It is assumed that
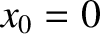 . In other words, the molecule is initially at the origin. We can write
. In other words, the molecule is initially at the origin. We can write
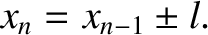 |
(5.43) |
Hence,
 |
(5.44) |
which implies that
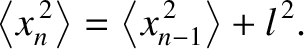 |
(5.45) |
Thus, by induction, after  steps, we obtain
steps, we obtain
 |
(5.46) |
Suppose that the steps are taken at a mean frequency 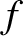 . It follows that
. It follows that 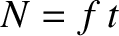 , where
, where
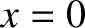 at
at  . Hence,
. Hence,
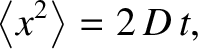 |
(5.47) |
where
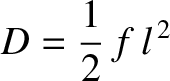 |
(5.48) |
is known as the diffusivity. According to Equation (5.47), the molecule's mean square distance from
its starting point grows linearly in time. This type of motion is known as diffusion. (See Section 5.3.9.)
Consider a random walk in three dimensions. Let  be the displacement of our molecule from the origin (which is
its starting point). Suppose that the molecule takes steps of
uniform length
be the displacement of our molecule from the origin (which is
its starting point). Suppose that the molecule takes steps of
uniform length  , in a random direction,
, in a random direction, 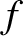 times a second. Let
times a second. Let  be the displacement
associated with a given step. Let
be the displacement
associated with a given step. Let 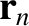 be the molecule's displacement after
be the molecule's displacement after  steps. We can write
steps. We can write
 |
(5.49) |
Thus,
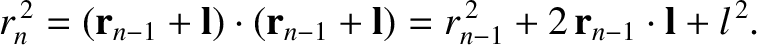 |
(5.50) |
However, if  is in a random direction then
is in a random direction then
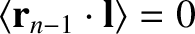 ,
because the cosine of the angle subtended between
,
because the cosine of the angle subtended between
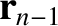 and
and  is
just as likely to be positive as to be negative. Hence, the average of the
previous equation yields
is
just as likely to be positive as to be negative. Hence, the average of the
previous equation yields
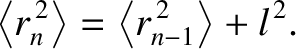 |
(5.51) |
By induction, after  steps, we obtain
steps, we obtain
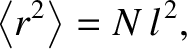 |
(5.52) |
which implies that
 |
(5.53) |
where
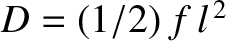 . Thus, the motion of the molecule is again diffusive in nature.
. Thus, the motion of the molecule is again diffusive in nature.
 along the
along the  -axis. Suppose, further, that the steps are taken to the left (i.e., in the negative
-axis. Suppose, further, that the steps are taken to the left (i.e., in the negative
 -direction) or to the
right, at random, with equal probabilities. Let
-direction) or to the
right, at random, with equal probabilities. Let 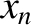 be the molecule's
be the molecule's  coordinate after
coordinate after  steps. It is assumed that
steps. It is assumed that
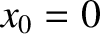 . In other words, the molecule is initially at the origin. We can write
. In other words, the molecule is initially at the origin. We can write
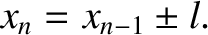

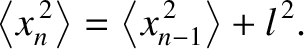
 steps, we obtain
steps, we obtain

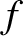 . It follows that
. It follows that 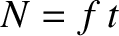 , where
, where
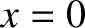 at
at  . Hence,
where
. Hence,
where
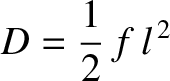
 be the displacement of our molecule from the origin (which is
its starting point). Suppose that the molecule takes steps of
uniform length
be the displacement of our molecule from the origin (which is
its starting point). Suppose that the molecule takes steps of
uniform length  , in a random direction,
, in a random direction, 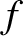 times a second. Let
times a second. Let  be the displacement
associated with a given step. Let
be the displacement
associated with a given step. Let 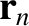 be the molecule's displacement after
be the molecule's displacement after  steps. We can write
steps. We can write

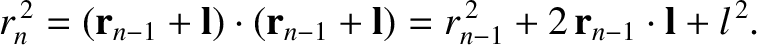
 is in a random direction then
is in a random direction then
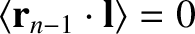 ,
because the cosine of the angle subtended between
,
because the cosine of the angle subtended between
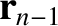 and
and  is
just as likely to be positive as to be negative. Hence, the average of the
previous equation yields
is
just as likely to be positive as to be negative. Hence, the average of the
previous equation yields
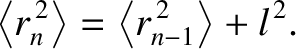
 steps, we obtain
steps, we obtain
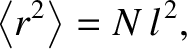

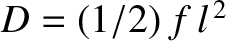 . Thus, the motion of the molecule is again diffusive in nature.
. Thus, the motion of the molecule is again diffusive in nature.