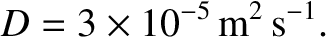Diffusion
Consider an ideal gas of uniform temperature,  , that has a number density gradient along the
, that has a number density gradient along the  -axis, such
that
-axis, such
that
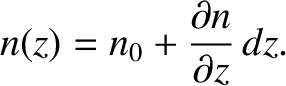 |
(5.230) |
Let  be the distribution of molecular speeds.
Repeating the analysis of Section 5.3.2, the number of molecules per unit area, per second, whose speeds lie between
be the distribution of molecular speeds.
Repeating the analysis of Section 5.3.2, the number of molecules per unit area, per second, whose speeds lie between
 and
and  , and whose directions of motion subtend an angle lying between
, and whose directions of motion subtend an angle lying between  and
and
 with the
with the  -axis, that cross the
-axis, that cross the  -
- plane is
plane is
![$\displaystyle dJ_z = [n'\,F(v)\,dv]\,[g(\theta)\,d\theta]\,[v_z] = \left[n'\,F(v)\,dv\right]\left[\frac{1}{2}\,\sin\theta\,d\theta\right][v\,\cos\theta],$](img3799.png) |
(5.231) |
where 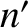 is the number density where the molecules last made a collision. [See Equation (5.167).] On average, the
molecules move a distance
is the number density where the molecules last made a collision. [See Equation (5.167).] On average, the
molecules move a distance  (i.e., the mean free path) between collisions. Hence,
(i.e., the mean free path) between collisions. Hence,
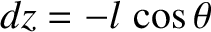 ,
and
,
and
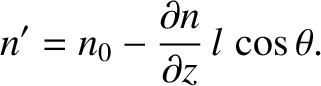 |
(5.232) |
Thus, the net flux of molecules across the  -
- plane is
plane is
![$\displaystyle J_z =\frac{1}{2}\int_0^\pi\left[n_0-\frac{\partial n}{\partial z}\,l\,\cos\theta\right]\cos\theta\,\sin\theta\,d\theta \int_0^\infty F(v)\,dv,$](img3802.png) |
(5.233) |
which gives
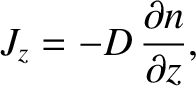 |
(5.234) |
where
 |
(5.235) |
Here,
 is the mean molecular speed. (See Section 5.5.9.)
Thus, we conclude that the flux of molecules in the
is the mean molecular speed. (See Section 5.5.9.)
Thus, we conclude that the flux of molecules in the  -direction is proportional to minus the local number density gradient along the
-direction is proportional to minus the local number density gradient along the  -axis. This
result is known as Fick's law, after Adolf Fick who discovered in experimentally in 1855.
-axis. This
result is known as Fick's law, after Adolf Fick who discovered in experimentally in 1855.
Consider a slab of gas lying between  and
and 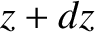 . The rate of change of the number of
molecules contained in the slab is the difference between the flux of molecules into the slab and the flux of
molecules out of the slab. In other words,
. The rate of change of the number of
molecules contained in the slab is the difference between the flux of molecules into the slab and the flux of
molecules out of the slab. In other words,
![$\displaystyle \frac{\partial (n\,A\,dz)}{\partial t}= \left[J_z(z,t)- J_z(z+dz,t)\right]A,$](img3806.png) |
(5.236) |
where  is the cross-sectional area of the slab. The previous equation implies that
is the cross-sectional area of the slab. The previous equation implies that
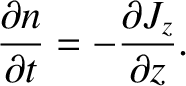 |
(5.237) |
However, making use of Fick's law, (5.234), we obtain
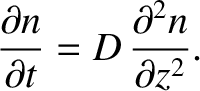 |
(5.238) |
The previous equation is known as the diffusion equation, and the constant 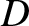 is known
as the diffusivity.
is known
as the diffusivity.
It can be seen, by inspection, that one solution of the diffusion equation is
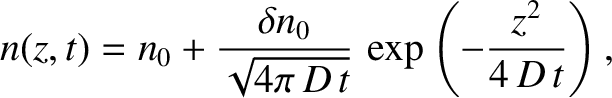 |
(5.239) |
where 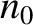 and
and
 are arbitrary constants.
Note that at
are arbitrary constants.
Note that at  ,
,
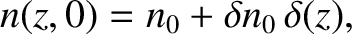 |
(5.240) |
where 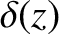 is a delta function. (See Section 2.1.6.)
Moreover, at large times,
is a delta function. (See Section 2.1.6.)
Moreover, at large times,
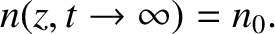 |
(5.241) |
Thus, our solution describes an initially
localized Gaussian (see Section 5.1.7) density perturbation that gradually spreads out, and eventually disperses entirely. It is easily demonstrated that the width (i.e., standard deviation) of the density perturbation, 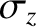 ,
grows in time as
,
grows in time as
 |
(5.242) |
On the other hand, the maximum height of the perturbation decays in time as
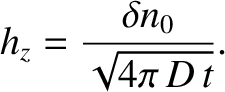 |
(5.243) |
Moreover, the area under the perturbation remains fixed as it evolves in time, which implies that the
number of molecules associated with the density perturbation also remains fixed, as has to be the
case (because we have not discussed any processes that create or destroy molecules).
It is clear, from Sections 5.1.5 and 5.1.7, that the spreading of the density perturbation is due to a
random walk of the excess molecules along the  -axis, under the action of molecular collisions.
-axis, under the action of molecular collisions.
Let us estimate the particle diffusivity in air at standard temperature (
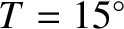 C) and pressure
(
C) and pressure
(
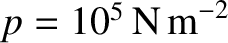 ).
The mean thermal speed of molecules of mass
).
The mean thermal speed of molecules of mass  in an ideal gas of temperature
in an ideal gas of temperature  is
is
 |
(5.244) |
(See Section 5.5.9.)
Hence, it follows from Equations (5.219), (5.220), and (5.235) that
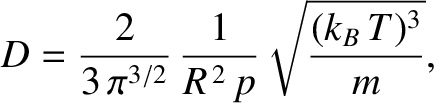 |
(5.245) |
where  is the molecular diameter. Thus, the diffusivity scales as
is the molecular diameter. Thus, the diffusivity scales as 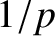 at constant temperature, as
at constant temperature, as
 at constant pressure, and as
at constant pressure, and as 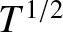 at constant volume. Given that
at constant volume. Given that 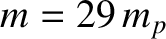 for air, where
for air, where 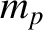 is the proton mass, and
is the proton mass, and
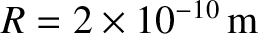 , we deduce that
, we deduce that
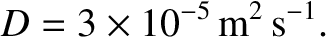 |
(5.246) |
This is a very small diffusivity. According to Equation (5.242), it takes about 4.6 hours for
a molecule to diffuse a distance of 1 meter in air.
 , that has a number density gradient along the
, that has a number density gradient along the  -axis, such
that
-axis, such
that
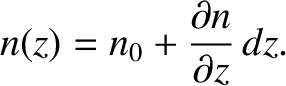
 be the distribution of molecular speeds.
Repeating the analysis of Section 5.3.2, the number of molecules per unit area, per second, whose speeds lie between
be the distribution of molecular speeds.
Repeating the analysis of Section 5.3.2, the number of molecules per unit area, per second, whose speeds lie between
 and
and  , and whose directions of motion subtend an angle lying between
, and whose directions of motion subtend an angle lying between  and
and
 with the
with the  -axis, that cross the
-axis, that cross the  -
- plane is
plane is
![$\displaystyle dJ_z = [n'\,F(v)\,dv]\,[g(\theta)\,d\theta]\,[v_z] = \left[n'\,F(v)\,dv\right]\left[\frac{1}{2}\,\sin\theta\,d\theta\right][v\,\cos\theta],$](img3799.png)
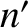 is the number density where the molecules last made a collision. [See Equation (5.167).] On average, the
molecules move a distance
is the number density where the molecules last made a collision. [See Equation (5.167).] On average, the
molecules move a distance  (i.e., the mean free path) between collisions. Hence,
(i.e., the mean free path) between collisions. Hence,
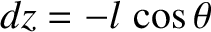 ,
and
,
and
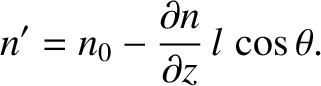
 -
- plane is
plane is
![$\displaystyle J_z =\frac{1}{2}\int_0^\pi\left[n_0-\frac{\partial n}{\partial z}\,l\,\cos\theta\right]\cos\theta\,\sin\theta\,d\theta \int_0^\infty F(v)\,dv,$](img3802.png)
 is the mean molecular speed. (See Section 5.5.9.)
Thus, we conclude that the flux of molecules in the
is the mean molecular speed. (See Section 5.5.9.)
Thus, we conclude that the flux of molecules in the  -direction is proportional to minus the local number density gradient along the
-direction is proportional to minus the local number density gradient along the  -axis. This
result is known as Fick's law, after Adolf Fick who discovered in experimentally in 1855.
-axis. This
result is known as Fick's law, after Adolf Fick who discovered in experimentally in 1855.
 and
and 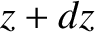 . The rate of change of the number of
molecules contained in the slab is the difference between the flux of molecules into the slab and the flux of
molecules out of the slab. In other words,
. The rate of change of the number of
molecules contained in the slab is the difference between the flux of molecules into the slab and the flux of
molecules out of the slab. In other words,
![$\displaystyle \frac{\partial (n\,A\,dz)}{\partial t}= \left[J_z(z,t)- J_z(z+dz,t)\right]A,$](img3806.png)
 is the cross-sectional area of the slab. The previous equation implies that
is the cross-sectional area of the slab. The previous equation implies that
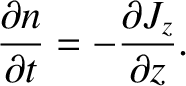
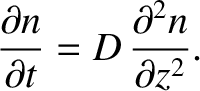
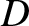 is known
as the diffusivity.
is known
as the diffusivity.
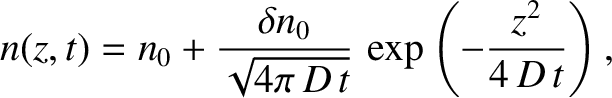
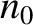 and
and
 are arbitrary constants.
Note that at
are arbitrary constants.
Note that at  ,
,
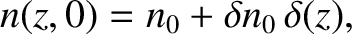
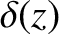 is a delta function. (See Section 2.1.6.)
Moreover, at large times,
is a delta function. (See Section 2.1.6.)
Moreover, at large times,
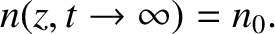
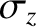 ,
grows in time as
On the other hand, the maximum height of the perturbation decays in time as
,
grows in time as
On the other hand, the maximum height of the perturbation decays in time as
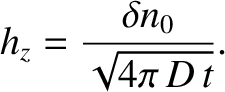
 -axis, under the action of molecular collisions.
-axis, under the action of molecular collisions.
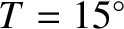 C) and pressure
(
C) and pressure
(
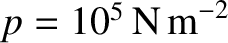 ).
The mean thermal speed of molecules of mass
).
The mean thermal speed of molecules of mass  in an ideal gas of temperature
in an ideal gas of temperature  is
is
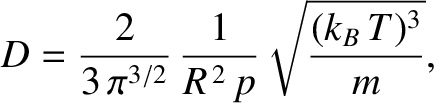
 is the molecular diameter. Thus, the diffusivity scales as
is the molecular diameter. Thus, the diffusivity scales as 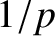 at constant temperature, as
at constant temperature, as
 at constant pressure, and as
at constant pressure, and as 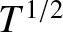 at constant volume. Given that
at constant volume. Given that 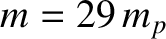 for air, where
for air, where 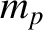 is the proton mass, and
is the proton mass, and
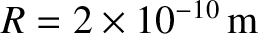 , we deduce that
, we deduce that