Next: Pressure Up: Kinetic Theory Previous: Fundamental Assumptions
 . (See Section 5.5.9.) In other words, the probability that a given molecule has
a speed in the range
. (See Section 5.5.9.) In other words, the probability that a given molecule has
a speed in the range  to
to  is
is  . Let
. Let  be the total number of molecules per unit volume.
Let us calculate how many molecules per unit area, per second, pass through the
be the total number of molecules per unit volume.
Let us calculate how many molecules per unit area, per second, pass through the  -
- plane in the direction of increasing
plane in the direction of increasing  . This quantity,
. This quantity,
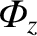 , is
termed the molecular flux.
, is
termed the molecular flux.
Let  and
and  be standard spherical polar angles.
(See Section A.23.) We can write the Cartesian components of the velocity of a given molecule, whose molecular speed is
be standard spherical polar angles.
(See Section A.23.) We can write the Cartesian components of the velocity of a given molecule, whose molecular speed is  , as
, as
 ,
,
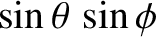 ,
,
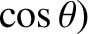 . If the
molecules are equally likely to move in any direction then the number of molecules for which
. If the
molecules are equally likely to move in any direction then the number of molecules for which  lies
between
lies
between  and
and
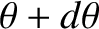 , and
, and  lies between
lies between  and
and
 , is proportional
to
, is proportional
to
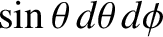 (i.e., to the amount of solid angle contained in this range of angles). Thus, the number of molecules for which
(i.e., to the amount of solid angle contained in this range of angles). Thus, the number of molecules for which  lies between
lies between
 and
and
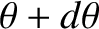 , and
, and  can take any value in the range 0 to
can take any value in the range 0 to 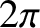 , is proportional
to
, is proportional
to
 . Hence, given that there are
. Hence, given that there are 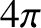 steradians in a complete solid angle,
the fraction of molecules for which
steradians in a complete solid angle,
the fraction of molecules for which  lies between
lies between  and
and
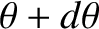 is
is
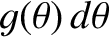 ,
where
,
where
Consider molecules whose speeds lie between  and
and  . The number of such molecules
per unit volume is
. The number of such molecules
per unit volume is
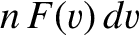 . The number of such molecules per unit volume
whose directions of motion subtend an angle lying between
. The number of such molecules per unit volume
whose directions of motion subtend an angle lying between  and
and
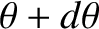 with the
with the  -axis is
-axis is
![$[n\,F(v)\,dv]\,[g(\theta)\,d\theta]$](img3705.png) . All such molecules for which
. All such molecules for which
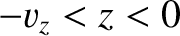 cross the
cross the  -
- plane
in one second.
Thus, the number of such molecules per unit area, per second, that
cross the
plane
in one second.
Thus, the number of such molecules per unit area, per second, that
cross the  -
- plane is
plane is
![$\displaystyle d{\mit\Phi}_z = [n\,F(v)\,dv]\,[g(\theta)\,d\theta]\,[v_z] = \left[n\,F(v)\,dv\right]\left[\frac{1}{2}\,\sin\theta\,d\theta\right][v\,\cos\theta].$](img3707.png) |
(5.168) |
 -
- plane in the direction of increasing
plane in the direction of increasing  (i.e., with
(i.e., with
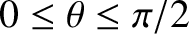 ) is
) is
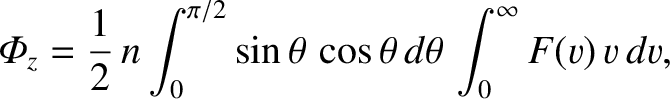 |
(5.169) |
 |
(5.171) |
For example, if a low-pressure gas is held in a container, the wall of which contains a small hole of
area  , then the number of escaping molecules per second is
, then the number of escaping molecules per second is