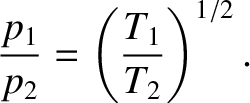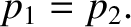Molecular Effusion
Consider an ideal gas held in a container that is divided in two by a partition. Let the gas to the left of the partition
have temperature 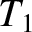 , pressure
, pressure 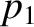 , and number density
, and number density 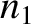 . Likewise, let the gas to the right of the partition
have temperature
. Likewise, let the gas to the right of the partition
have temperature 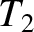 , pressure
, pressure 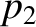 , and number density
, and number density  . Suppose that the partition contains a small hole of cross-sectional
area
. Suppose that the partition contains a small hole of cross-sectional
area  . Suppose that the dimension of the hole is much less than the mean free path between collisions
for the gases on either side of the partition. In this case, as described in Section 5.3.2, the gases effuse through the hole, rather than flowing through it in a hydrodynamical fashion.
. Suppose that the dimension of the hole is much less than the mean free path between collisions
for the gases on either side of the partition. In this case, as described in Section 5.3.2, the gases effuse through the hole, rather than flowing through it in a hydrodynamical fashion.
According to Equations (5.172), (5.244), and the ideal gas law, which states that
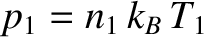 , the number of molecules per unit time that effuse from the
left partition to the right partition is
, the number of molecules per unit time that effuse from the
left partition to the right partition is
 |
(5.284) |
where  is the molecular mass. Likewise, the number of molecules per unit time that effuse from the
right partition to the left partition is
is the molecular mass. Likewise, the number of molecules per unit time that effuse from the
right partition to the left partition is
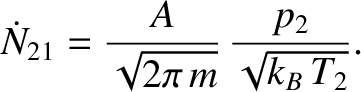 |
(5.285) |
In a steady state, we require
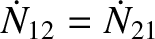 . Hence, we deduce that
. Hence, we deduce that
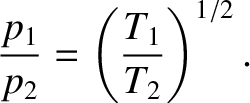 |
(5.286) |
Thus, in equilibrium, a higher pressure prevails in the part of the container held at a higher temperature.
This result is different to that we would obtain in limit in which the mean free path is much less than the size of
the hole. In this limit, the gases on either side of the hole flow through it in a hydrodynamical fashion, and
an equilibrium state is achieved when
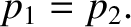 |
(5.287) |
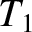 , pressure
, pressure 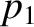 , and number density
, and number density 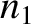 . Likewise, let the gas to the right of the partition
have temperature
. Likewise, let the gas to the right of the partition
have temperature 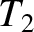 , pressure
, pressure 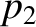 , and number density
, and number density  . Suppose that the partition contains a small hole of cross-sectional
area
. Suppose that the partition contains a small hole of cross-sectional
area  . Suppose that the dimension of the hole is much less than the mean free path between collisions
for the gases on either side of the partition. In this case, as described in Section 5.3.2, the gases effuse through the hole, rather than flowing through it in a hydrodynamical fashion.
. Suppose that the dimension of the hole is much less than the mean free path between collisions
for the gases on either side of the partition. In this case, as described in Section 5.3.2, the gases effuse through the hole, rather than flowing through it in a hydrodynamical fashion.
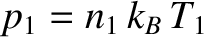 , the number of molecules per unit time that effuse from the
left partition to the right partition is
, the number of molecules per unit time that effuse from the
left partition to the right partition is

 is the molecular mass. Likewise, the number of molecules per unit time that effuse from the
right partition to the left partition is
is the molecular mass. Likewise, the number of molecules per unit time that effuse from the
right partition to the left partition is
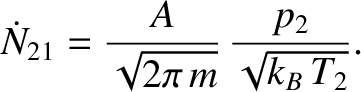
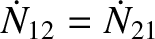 . Hence, we deduce that
. Hence, we deduce that