Consider the flow of an ideal gas down a uniform pipe of circular cross-section in the limit that the gas pressure is sufficiently
low that the mean free path between collisions greatly exceeds the diameter of the pipe. This type of flow is
known as molecular flow.
Suppose that the pipe runs along the  -axis, and that a pressure difference,
-axis, and that a pressure difference,
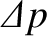 , is established between the
two ends of the pipe, in order to drive the flow. The temperature of the gas is assumed to be uniform along the pipe. Finally, the length of the pipe,
, is established between the
two ends of the pipe, in order to drive the flow. The temperature of the gas is assumed to be uniform along the pipe. Finally, the length of the pipe, 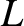 , is assumed to be much greater than
its diameter,
, is assumed to be much greater than
its diameter, 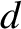 .
Making use of Equation (5.170), the net flux of molecules down the pipe at position
.
Making use of Equation (5.170), the net flux of molecules down the pipe at position  is
is
![$\displaystyle {\mit\Phi}_z(z)= \frac{1}{4}\,\langle v\rangle\left[n(z-d)-n(z+d)\right],$](img3866.png) |
(5.274) |
where
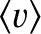 is the mean molecular speed [which is constant because it only depends on the temperature; see Equation (5.433)], and
is the mean molecular speed [which is constant because it only depends on the temperature; see Equation (5.433)], and 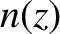 the molecular number density.
The right-hand side of the previous equation represents the difference between the particle flux in the
the molecular number density.
The right-hand side of the previous equation represents the difference between the particle flux in the 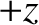 -direction
and that in the
-direction
and that in the 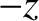 -direction. The former flux is characterized by the value the number density calculated at the position at which the molecules
moving in the
-direction. The former flux is characterized by the value the number density calculated at the position at which the molecules
moving in the 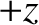 direction
last collided with the wall of the pipe, which is estimated to be
direction
last collided with the wall of the pipe, which is estimated to be  . Likewise, the latter flux is characterized by the number density calculated at the position at which the molecules
moving in the
. Likewise, the latter flux is characterized by the number density calculated at the position at which the molecules
moving in the 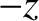 direction
last collided with the wall of the pipe, which is estimated to be
direction
last collided with the wall of the pipe, which is estimated to be  . According to Equation (5.175),
the pressure of the gas in the pipe is
. According to Equation (5.175),
the pressure of the gas in the pipe is
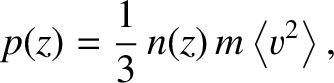 |
(5.275) |
where  is the molecular mass, and
is the molecular mass, and
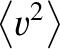 is the mean square molecular speed (which is also constant because it only depends on the temperature). [See Equation (5.434).] The previous two equations yield
In a steady state,
is the mean square molecular speed (which is also constant because it only depends on the temperature). [See Equation (5.434).] The previous two equations yield
In a steady state,
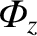 must be uniform along the pipe, which implies that
must be uniform along the pipe, which implies that 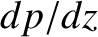 is also uniform.
Hence, we can write
is also uniform.
Hence, we can write
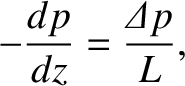 |
(5.277) |
which yields
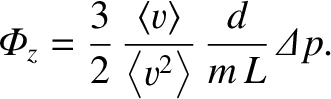 |
(5.278) |
Now, the cross-sectional area of the pipe is
 . Hence, the rate of mass flow down the
pipe is
. Hence, the rate of mass flow down the
pipe is
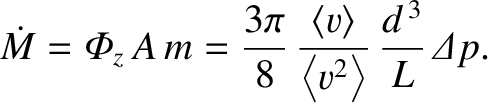 |
(5.279) |
However, in a ideal gas,
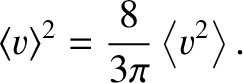 |
(5.280) |
(See Section 5.5.9.)
Thus, we obtain
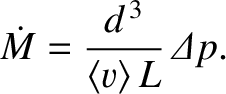 |
(5.281) |
Given that
 [see Equation (5.244)], where
[see Equation (5.244)], where  is the temperature of the gas, we deduce that the mass flow
rate due to molecular flow of an ideal gas down a pipe, when a given pressure difference is established between the
two ends of the pipe, is proportional to the cube of the pipe diameter, inversely
proportional to the length of the pipe, and inversely proportional to the square-root of the temperature.
is the temperature of the gas, we deduce that the mass flow
rate due to molecular flow of an ideal gas down a pipe, when a given pressure difference is established between the
two ends of the pipe, is proportional to the cube of the pipe diameter, inversely
proportional to the length of the pipe, and inversely proportional to the square-root of the temperature.
Now, the standard formula for the mass flow rate of a viscous fluid down a pipe of circular
cross-section, which applies to the case under discussion when the mean free path between collisions is much less than the diameter
of the pipe, is
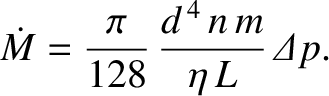 |
(5.282) |
Making use of Equation (5.266), we deduce that the mass flow rate of an ideal gas down a pipe of circular
cross-section, in the short mean free
path limit, is
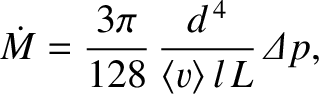 |
(5.283) |
where  is the mean free path. Thus, Equation (5.281) holds when
is the mean free path. Thus, Equation (5.281) holds when 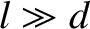 , and
Equation (5.283) holds when
, and
Equation (5.283) holds when 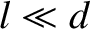 .
.
 -axis, and that a pressure difference,
-axis, and that a pressure difference,
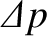 , is established between the
two ends of the pipe, in order to drive the flow. The temperature of the gas is assumed to be uniform along the pipe. Finally, the length of the pipe,
, is established between the
two ends of the pipe, in order to drive the flow. The temperature of the gas is assumed to be uniform along the pipe. Finally, the length of the pipe, 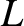 , is assumed to be much greater than
its diameter,
, is assumed to be much greater than
its diameter, 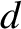 .
Making use of Equation (5.170), the net flux of molecules down the pipe at position
.
Making use of Equation (5.170), the net flux of molecules down the pipe at position  is
is
![$\displaystyle {\mit\Phi}_z(z)= \frac{1}{4}\,\langle v\rangle\left[n(z-d)-n(z+d)\right],$](img3866.png)
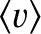 is the mean molecular speed [which is constant because it only depends on the temperature; see Equation (5.433)], and
is the mean molecular speed [which is constant because it only depends on the temperature; see Equation (5.433)], and 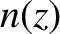 the molecular number density.
The right-hand side of the previous equation represents the difference between the particle flux in the
the molecular number density.
The right-hand side of the previous equation represents the difference between the particle flux in the 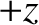 -direction
and that in the
-direction
and that in the 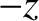 -direction. The former flux is characterized by the value the number density calculated at the position at which the molecules
moving in the
-direction. The former flux is characterized by the value the number density calculated at the position at which the molecules
moving in the 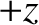 direction
last collided with the wall of the pipe, which is estimated to be
direction
last collided with the wall of the pipe, which is estimated to be  . Likewise, the latter flux is characterized by the number density calculated at the position at which the molecules
moving in the
. Likewise, the latter flux is characterized by the number density calculated at the position at which the molecules
moving in the 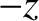 direction
last collided with the wall of the pipe, which is estimated to be
direction
last collided with the wall of the pipe, which is estimated to be  . According to Equation (5.175),
the pressure of the gas in the pipe is
. According to Equation (5.175),
the pressure of the gas in the pipe is
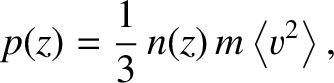
 is the molecular mass, and
is the molecular mass, and
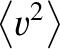 is the mean square molecular speed (which is also constant because it only depends on the temperature). [See Equation (5.434).] The previous two equations yield
is the mean square molecular speed (which is also constant because it only depends on the temperature). [See Equation (5.434).] The previous two equations yield

![$\displaystyle = \frac{3}{4}\,\frac{\langle v\rangle}{m\,\left\langle v^2\right\rangle}\left[p(z-d)-p(z+d)\right]$](img3873.png)
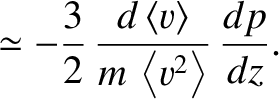
 must be uniform along the pipe, which implies that
must be uniform along the pipe, which implies that  is also uniform.
Hence, we can write
is also uniform.
Hence, we can write
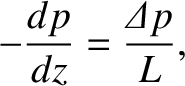
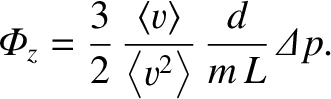
 . Hence, the rate of mass flow down the
pipe is
. Hence, the rate of mass flow down the
pipe is
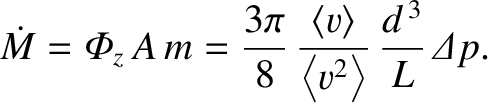
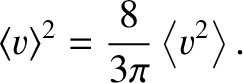
 [see Equation (5.244)], where
[see Equation (5.244)], where  is the temperature of the gas, we deduce that the mass flow
rate due to molecular flow of an ideal gas down a pipe, when a given pressure difference is established between the
two ends of the pipe, is proportional to the cube of the pipe diameter, inversely
proportional to the length of the pipe, and inversely proportional to the square-root of the temperature.
is the temperature of the gas, we deduce that the mass flow
rate due to molecular flow of an ideal gas down a pipe, when a given pressure difference is established between the
two ends of the pipe, is proportional to the cube of the pipe diameter, inversely
proportional to the length of the pipe, and inversely proportional to the square-root of the temperature.
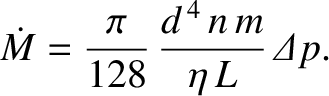
 is the mean free path. Thus, Equation (5.281) holds when
is the mean free path. Thus, Equation (5.281) holds when 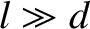 , and
Equation (5.283) holds when
, and
Equation (5.283) holds when 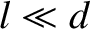 .
.