Pressure
Suppose that the  -
- plane actually corresponds to a wall of the container.
Consider, again, molecules whose speeds lie between
plane actually corresponds to a wall of the container.
Consider, again, molecules whose speeds lie between  and
and  , and
whose directions of motion subtend an angle lying between
, and
whose directions of motion subtend an angle lying between  and
and
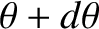 with the
with the  -axis.
Each such molecule
that encounters the wall bounces off it in a specular fashion, and its
-axis.
Each such molecule
that encounters the wall bounces off it in a specular fashion, and its  -momentum consequently
changes by
-momentum consequently
changes by 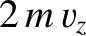 , where
, where  is the molecular mass. Thus, the normal reaction force per unit area
acting on the wall is
is the molecular mass. Thus, the normal reaction force per unit area
acting on the wall is
![$\displaystyle dp =[2\,m\,v_z]\,[n\,F(v)\,dv] \,[g(\theta)\,d\theta]\,[v_z]=\,[2...
...n\,F(v)\,dv\right]\left[\frac{1}{2}\,\sin\theta\,d\theta\right][v\,\cos\theta].$](img3714.png) |
(5.173) |
[See Equation (5.167).]
Hence, the total pressure exerted on the wall is
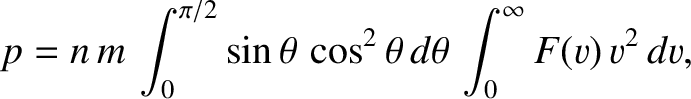 |
(5.174) |
which reduces to
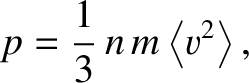 |
(5.175) |
where
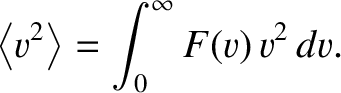 |
(5.176) |
is the mean square molecular speed. (See Section 5.5.9.)
However, we can write
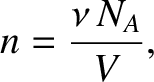 |
(5.177) |
where 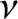 is the number of moles of molecules held inside the container,
is the number of moles of molecules held inside the container,  is the volume of the container,
and
is the volume of the container,
and  is Avogadro's number. Equations (5.175) and (5.177) yield
is Avogadro's number. Equations (5.175) and (5.177) yield
 |
(5.178) |
where
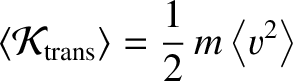 |
(5.179) |
is the mean translational kinetic energy of a molecule in the gas.
Equation (5.178) is consistent with the ideal gas law, (5.97), provided that
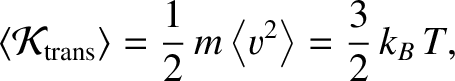 |
(5.180) |
where 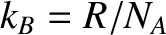 is the Boltzmann constant. [See Equation (5.100).]
is the Boltzmann constant. [See Equation (5.100).]
 -
- plane actually corresponds to a wall of the container.
Consider, again, molecules whose speeds lie between
plane actually corresponds to a wall of the container.
Consider, again, molecules whose speeds lie between  and
and  , and
whose directions of motion subtend an angle lying between
, and
whose directions of motion subtend an angle lying between  and
and
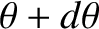 with the
with the  -axis.
Each such molecule
that encounters the wall bounces off it in a specular fashion, and its
-axis.
Each such molecule
that encounters the wall bounces off it in a specular fashion, and its  -momentum consequently
changes by
-momentum consequently
changes by 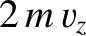 , where
, where  is the molecular mass. Thus, the normal reaction force per unit area
acting on the wall is
is the molecular mass. Thus, the normal reaction force per unit area
acting on the wall is
![$\displaystyle dp =[2\,m\,v_z]\,[n\,F(v)\,dv] \,[g(\theta)\,d\theta]\,[v_z]=\,[2...
...n\,F(v)\,dv\right]\left[\frac{1}{2}\,\sin\theta\,d\theta\right][v\,\cos\theta].$](img3714.png)
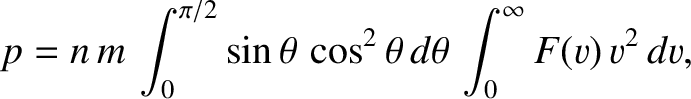
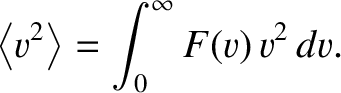
 is the number of moles of molecules held inside the container,
is the number of moles of molecules held inside the container,  is the volume of the container,
and
is the volume of the container,
and  is Avogadro's number. Equations (5.175) and (5.177) yield
where
is Avogadro's number. Equations (5.175) and (5.177) yield
where
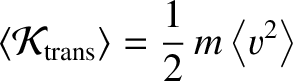
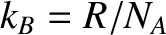 is the Boltzmann constant. [See Equation (5.100).]
is the Boltzmann constant. [See Equation (5.100).]