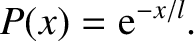Mean Free Path
The mean free path is the average distance a molecule in a gas travels between collisions with
other molecules. Let us crudely approximate the molecules in the gas as hard spheres of diameter  . Any two molecules whose
centers are less than a distance
. Any two molecules whose
centers are less than a distance  apart will collide. Suppose that one molecule is moving with
velocity
apart will collide. Suppose that one molecule is moving with
velocity  , whereas the other molecules are stationary. The moving molecule
sweeps out a cylindrical volume
, whereas the other molecules are stationary. The moving molecule
sweeps out a cylindrical volume
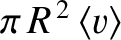 in one second. Any other molecule whose
center lies in this volume will collide with the moving molecule. There are
in one second. Any other molecule whose
center lies in this volume will collide with the moving molecule. There are
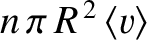 such molecules, where
such molecules, where  is the number density of molecules. Hence, the number of collisions
per second is
is the number density of molecules. Hence, the number of collisions
per second is
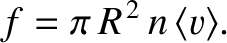 |
(5.209) |
Thus, the mean distance that the molecule travels between collisions, which is the mean free path,
is
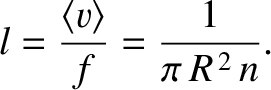 |
(5.210) |
If we now take into account the fact that all of the molecules in the gas are moving then it is clear that
the previous two equation generalize to give
where 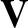 is the relative velocity between molecules. Consider two molecules of
velocities
is the relative velocity between molecules. Consider two molecules of
velocities 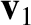 and
and 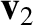 . The relative velocity of the molecules is
. The relative velocity of the molecules is
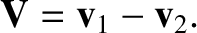 |
(5.213) |
Now,
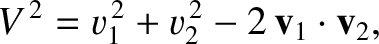 |
(5.214) |
which implies that
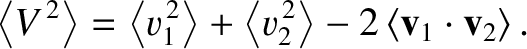 |
(5.215) |
However,
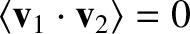 , because the cosine of the angle
subtended between
, because the cosine of the angle
subtended between 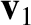 and
and 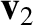 is just as likely to be positive as to be negative.
Thus, we deduce that
is just as likely to be positive as to be negative.
Thus, we deduce that
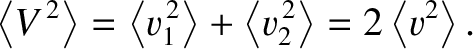 |
(5.216) |
Assuming, as seems reasonable, that
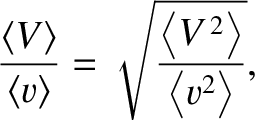 |
(5.217) |
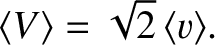 |
(5.218) |
Hence, Equation (5.212) yields
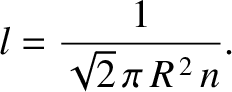 |
(5.219) |
Let us estimate the mean free path in air at standard temperature (
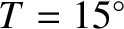 C) and pressure
(
C) and pressure
(
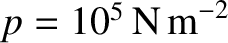 .) From the idea gas law, (5.97),
.) From the idea gas law, (5.97),
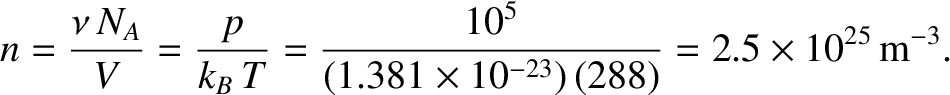 |
(5.220) |
Now,
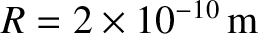 is a typical diameter of an air molecule. Thus, we obtain
is a typical diameter of an air molecule. Thus, we obtain
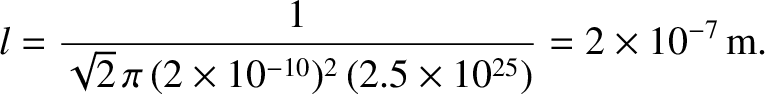 |
(5.221) |
Consider a molecule moving along the  -axis. The molecule is subject to random collisions. Thus, the
probability that the molecule undergoes a collision between moving a distance
-axis. The molecule is subject to random collisions. Thus, the
probability that the molecule undergoes a collision between moving a distance  and moving a distance
and moving a distance  is
is
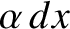 , where
, where  is a constant. Let
is a constant. Let 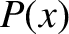 be the probability that the molecule
moves a distance
be the probability that the molecule
moves a distance  without undergoing a collision. It is evident that the probability that
the molecule's first collision occurs between moving a distance
without undergoing a collision. It is evident that the probability that
the molecule's first collision occurs between moving a distance  and a distance
and a distance  is
is
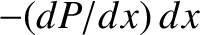 . However,
this probability is also equal to the probability that the molecule does not undergo
a collision in moving a distance
. However,
this probability is also equal to the probability that the molecule does not undergo
a collision in moving a distance  , and then undergoes a collision between moving a distance
, and then undergoes a collision between moving a distance  and a
distance
and a
distance  .
In other words,
.
In other words,
![$\displaystyle -\frac{dP}{dx}\,dx = [P(x)]\,[\alpha\,dx],$](img3788.png) |
(5.222) |
or
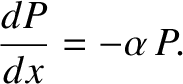 |
(5.223) |
The previous equation can be integrated to give
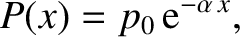 |
(5.224) |
where 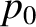 is an arbitrary constant. However,
is an arbitrary constant. However,  , because the molecule has no chance of undergoing
a collision in moving zero distance. Hence, the probability that the molecule moves a distance
, because the molecule has no chance of undergoing
a collision in moving zero distance. Hence, the probability that the molecule moves a distance  without
undergoing a collision is
without
undergoing a collision is
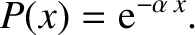 |
(5.225) |
Moreover, the probability that the molecule undergoes its first collision between moving a distance  and moving a distance
and moving a distance  is
is
![$f(x)\,dx = [P(x)]\,[\alpha\,dx]$](img3793.png) (i.e., the molecule needs to not
undergo a collision in moving a distance
(i.e., the molecule needs to not
undergo a collision in moving a distance  , and then undergo a collision between moving a distance
, and then undergo a collision between moving a distance  and a distance
and a distance  ), so
), so
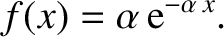 |
(5.226) |
The mean distance that the molecule travels before undergoing its first collision is (see Section 5.1.6)
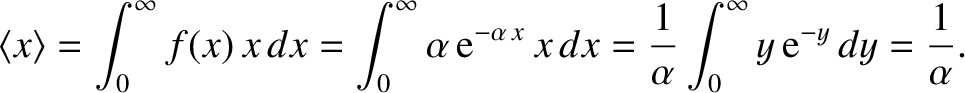 |
(5.227) |
However,
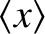 is equivalent to the mean free path,
is equivalent to the mean free path,  . Hence, the probability density for
a molecule to move a distance
. Hence, the probability density for
a molecule to move a distance  between collisions is
between collisions is
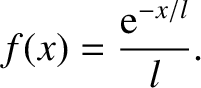 |
(5.228) |
Moreover, the probability that the molecule moves a distance  without undergoing a collision is
without undergoing a collision is
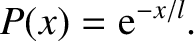 |
(5.229) |
 . Any two molecules whose
centers are less than a distance
. Any two molecules whose
centers are less than a distance  apart will collide. Suppose that one molecule is moving with
velocity
apart will collide. Suppose that one molecule is moving with
velocity  , whereas the other molecules are stationary. The moving molecule
sweeps out a cylindrical volume
, whereas the other molecules are stationary. The moving molecule
sweeps out a cylindrical volume
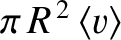 in one second. Any other molecule whose
center lies in this volume will collide with the moving molecule. There are
in one second. Any other molecule whose
center lies in this volume will collide with the moving molecule. There are
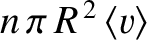 such molecules, where
such molecules, where  is the number density of molecules. Hence, the number of collisions
per second is
is the number density of molecules. Hence, the number of collisions
per second is
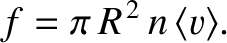
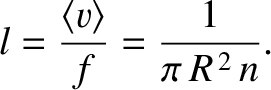
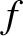
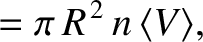
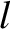
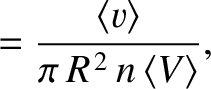
 is the relative velocity between molecules. Consider two molecules of
velocities
is the relative velocity between molecules. Consider two molecules of
velocities 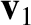 and
and 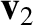 . The relative velocity of the molecules is
. The relative velocity of the molecules is
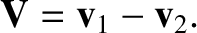
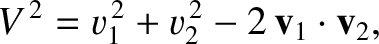
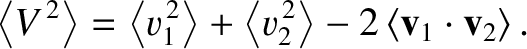
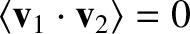 , because the cosine of the angle
subtended between
, because the cosine of the angle
subtended between 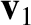 and
and 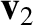 is just as likely to be positive as to be negative.
Thus, we deduce that
is just as likely to be positive as to be negative.
Thus, we deduce that
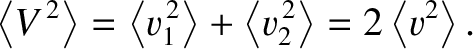
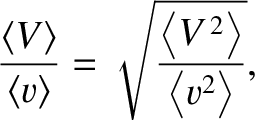
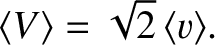
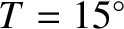 C) and pressure
(
C) and pressure
(
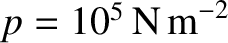 .) From the idea gas law, (5.97),
.) From the idea gas law, (5.97),
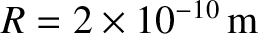 is a typical diameter of an air molecule. Thus, we obtain
is a typical diameter of an air molecule. Thus, we obtain
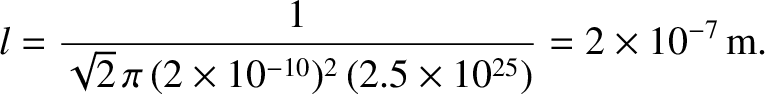
 -axis. The molecule is subject to random collisions. Thus, the
probability that the molecule undergoes a collision between moving a distance
-axis. The molecule is subject to random collisions. Thus, the
probability that the molecule undergoes a collision between moving a distance  and moving a distance
and moving a distance  is
is
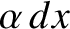 , where
, where  is a constant. Let
is a constant. Let 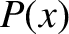 be the probability that the molecule
moves a distance
be the probability that the molecule
moves a distance  without undergoing a collision. It is evident that the probability that
the molecule's first collision occurs between moving a distance
without undergoing a collision. It is evident that the probability that
the molecule's first collision occurs between moving a distance  and a distance
and a distance  is
is
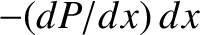 . However,
this probability is also equal to the probability that the molecule does not undergo
a collision in moving a distance
. However,
this probability is also equal to the probability that the molecule does not undergo
a collision in moving a distance  , and then undergoes a collision between moving a distance
, and then undergoes a collision between moving a distance  and a
distance
and a
distance  .
In other words,
.
In other words,
![$\displaystyle -\frac{dP}{dx}\,dx = [P(x)]\,[\alpha\,dx],$](img3788.png)
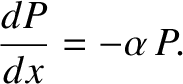
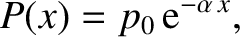
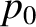 is an arbitrary constant. However,
is an arbitrary constant. However,  , because the molecule has no chance of undergoing
a collision in moving zero distance. Hence, the probability that the molecule moves a distance
, because the molecule has no chance of undergoing
a collision in moving zero distance. Hence, the probability that the molecule moves a distance  without
undergoing a collision is
without
undergoing a collision is
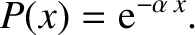
 and moving a distance
and moving a distance  is
is
![$f(x)\,dx = [P(x)]\,[\alpha\,dx]$](img3793.png) (i.e., the molecule needs to not
undergo a collision in moving a distance
(i.e., the molecule needs to not
undergo a collision in moving a distance  , and then undergo a collision between moving a distance
, and then undergo a collision between moving a distance  and a distance
and a distance  ), so
), so
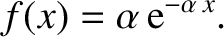
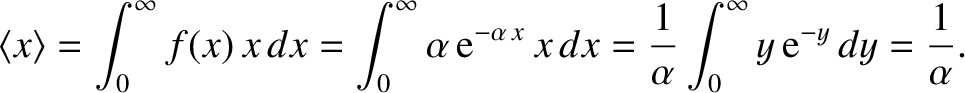
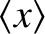 is equivalent to the mean free path,
is equivalent to the mean free path,  . Hence, the probability density for
a molecule to move a distance
. Hence, the probability density for
a molecule to move a distance  between collisions is
between collisions is
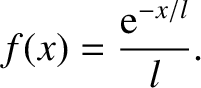
 without undergoing a collision is
without undergoing a collision is