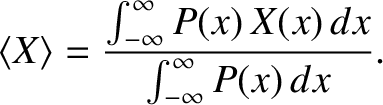Continuous Probability Distribution
Consider some physical system  . Suppose that a measurement of a particular physical property of this
system,
. Suppose that a measurement of a particular physical property of this
system,  , can result in a continuous range of different outcomes such that
, can result in a continuous range of different outcomes such that
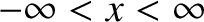 .
Now, we would expect the probability that a measurement of
.
Now, we would expect the probability that a measurement of  yields a result in the range
yields a result in the range  to
to  to be proportional to
to be proportional to 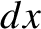 , in the limit that
, in the limit that
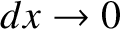 . (See Section 5.1.7.) Hence, we
can define the probability density,
. (See Section 5.1.7.) Hence, we
can define the probability density, 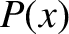 , such that the probability of a measurement of
, such that the probability of a measurement of
 yielding a result in the range
yielding a result in the range  to
to  is
is  . A simple extension of the result (5.3)
yields the normalization condition,
. A simple extension of the result (5.3)
yields the normalization condition,
 |
(5.54) |
It follows, from a straightforward extension of the results in Section 5.1.3 that
the mean value of  is
is
 |
(5.55) |
the mean value of 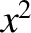 is
is
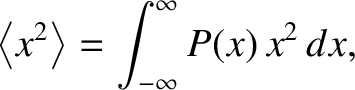 |
(5.56) |
and the variance of  is again
is again
 |
(5.57) |
If 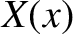 is some function of
is some function of  then
then
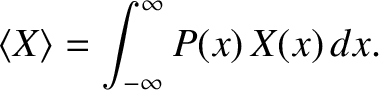 |
(5.58) |
Moreover, if 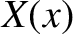 and
and 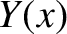 are independent functions of
are independent functions of  then
then
 |
(5.59) |
Finally, in some situations it is convenient to use a probability density, 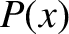 , that does not satisfy the normalization condition (5.54).
In such situations,
, that does not satisfy the normalization condition (5.54).
In such situations,
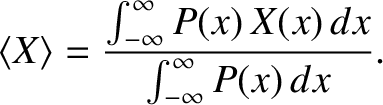 |
(5.60) |
 . Suppose that a measurement of a particular physical property of this
system,
. Suppose that a measurement of a particular physical property of this
system,  , can result in a continuous range of different outcomes such that
, can result in a continuous range of different outcomes such that
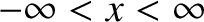 .
Now, we would expect the probability that a measurement of
.
Now, we would expect the probability that a measurement of  yields a result in the range
yields a result in the range  to
to  to be proportional to
to be proportional to 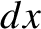 , in the limit that
, in the limit that
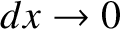 . (See Section 5.1.7.) Hence, we
can define the probability density,
. (See Section 5.1.7.) Hence, we
can define the probability density, 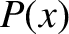 , such that the probability of a measurement of
, such that the probability of a measurement of
 yielding a result in the range
yielding a result in the range  to
to  is
is  . A simple extension of the result (5.3)
yields the normalization condition,
It follows, from a straightforward extension of the results in Section 5.1.3 that
the mean value of
. A simple extension of the result (5.3)
yields the normalization condition,
It follows, from a straightforward extension of the results in Section 5.1.3 that
the mean value of  is
is

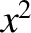 is
is
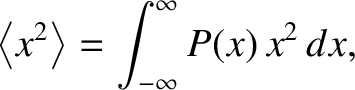
 is again
is again

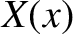 is some function of
is some function of  then
then
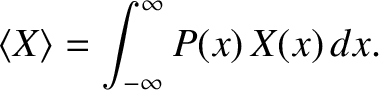
 and
and  are independent functions of
are independent functions of  then
then

 , that does not satisfy the normalization condition (5.54).
In such situations,
, that does not satisfy the normalization condition (5.54).
In such situations,