Thermal Conductivity
Consider a gas of uniform number density,  , that has a temperature gradient along the
, that has a temperature gradient along the  -axis, such that
-axis, such that
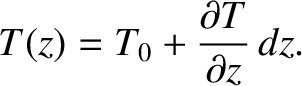 |
(5.247) |
Let each molecule in the gas have a mean thermal energy
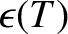 (under most circumstances this energy
is the sum of the molecule's translational and rotational kinetic energy). Slightly modifying the analysis of the previous
section, the thermal energy per unit area, per second, carried by molecules whose speeds lie between
(under most circumstances this energy
is the sum of the molecule's translational and rotational kinetic energy). Slightly modifying the analysis of the previous
section, the thermal energy per unit area, per second, carried by molecules whose speeds lie between
 and
and  , and whose directions of motion subtend an angle lying between
, and whose directions of motion subtend an angle lying between  and
and
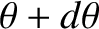 with the
with the  -axis, that cross the
-axis, that cross the  -
- plane, is
plane, is
![$\displaystyle dq_z= [\epsilon']\left[n\,F(v)\,dv\right]\left[\frac{1}{2}\,\sin\theta\,d\theta\right][v\,\cos\theta],$](img3827.png) |
(5.248) |
where  is the distribution of molecular speeds, and
is the distribution of molecular speeds, and
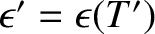 , where
, where 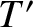 is the temperature where the molecules
last made a collision.
On average, the
molecules move a distance
is the temperature where the molecules
last made a collision.
On average, the
molecules move a distance  (i.e., the mean free path) between collisions. Hence,
(i.e., the mean free path) between collisions. Hence,
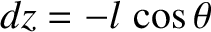 ,
and
,
and
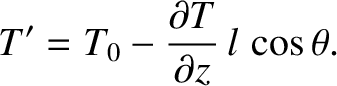 |
(5.249) |
which implies that
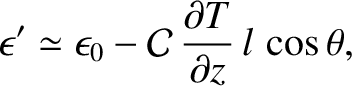 |
(5.250) |
where
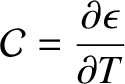 |
(5.251) |
is the specific heat per molecule.
Thus, the net heat flux across the  -
- plane is
plane is
![$\displaystyle q_z =\frac{n}{2}\int_0^\pi\left[\epsilon_0-{\cal C}\,\frac{\parti...
...z}\,l\,\cos\theta\right]\cos\theta\,\sin\theta\,d\theta \int_0^\infty F(v)\,dv,$](img3833.png) |
(5.252) |
which gives
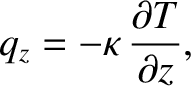 |
(5.253) |
where
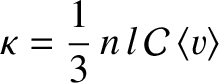 |
(5.254) |
is termed the thermal conductivity. Here,
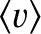 is the mean molecular speed. (See Section 5.5.9.) Thus, we conclude that the heat flux in the
is the mean molecular speed. (See Section 5.5.9.) Thus, we conclude that the heat flux in the  -direction is proportional to minus the local temperature gradient along the
-direction is proportional to minus the local temperature gradient along the  -axis. This is another example of Fick's law.
-axis. This is another example of Fick's law.
Equations (5.219), (5.244), and (5.253)
yield
 |
(5.255) |
where  is the molecular diameter, and
is the molecular diameter, and  the molecular mass. Moreover, for a
diatomic gas, such as air,
the molecular mass. Moreover, for a
diatomic gas, such as air,
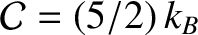 . (See Section 5.3.6.) It can be seen that the thermal conductivity of an ideal gas scales as
. (See Section 5.3.6.) It can be seen that the thermal conductivity of an ideal gas scales as 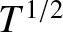 , and
is independent of the pressure at constant temperature.
The previous formula yields the following estimate for the thermal conductivity of air (assuming that
, and
is independent of the pressure at constant temperature.
The previous formula yields the following estimate for the thermal conductivity of air (assuming that
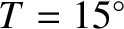 C,
C,
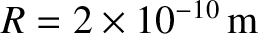 , and
, and 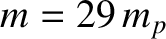 ),
),
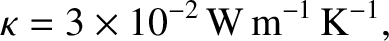 |
(5.256) |
which turns out to be fairly accurate
Consider a slab of gas lying between  and
and 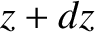 . The rate of change of the thermal energy contained in the slab is the difference between the flux of heat into the slab and the flux of
heat out of the slab. In other words,
. The rate of change of the thermal energy contained in the slab is the difference between the flux of heat into the slab and the flux of
heat out of the slab. In other words,
![$\displaystyle \frac{\partial (n\,A\,dz\,{\cal C}\,T)}{\partial t} = \left[q_z(z,t)- q_z(z+dz,t)\right]A,$](img3839.png) |
(5.257) |
where  is the cross-sectional area of the slab. It follows that
is the cross-sectional area of the slab. It follows that
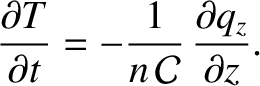 |
(5.258) |
Making use of Equations (5.253) and (5.254), we obtain
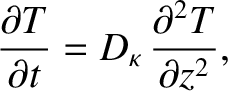 |
(5.259) |
where
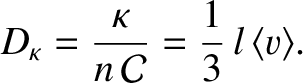 |
(5.260) |
Of course, Equation (5.259) is the diffusion equation, and 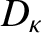 is the associated diffusivity.
Thus, we conclude, by comparison with the analysis in the previous section, that heat diffuses through
an ideal gas at the same very slow rate at which molecules diffuse. Moreover, it is clear, from Sections 5.1.5 and 5.1.7, that heat diffusion is due to a
random walk of molecules with excess energy under the action of molecular collisions.
is the associated diffusivity.
Thus, we conclude, by comparison with the analysis in the previous section, that heat diffuses through
an ideal gas at the same very slow rate at which molecules diffuse. Moreover, it is clear, from Sections 5.1.5 and 5.1.7, that heat diffusion is due to a
random walk of molecules with excess energy under the action of molecular collisions.
 , that has a temperature gradient along the
, that has a temperature gradient along the  -axis, such that
-axis, such that
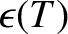 (under most circumstances this energy
is the sum of the molecule's translational and rotational kinetic energy). Slightly modifying the analysis of the previous
section, the thermal energy per unit area, per second, carried by molecules whose speeds lie between
(under most circumstances this energy
is the sum of the molecule's translational and rotational kinetic energy). Slightly modifying the analysis of the previous
section, the thermal energy per unit area, per second, carried by molecules whose speeds lie between
 and
and  , and whose directions of motion subtend an angle lying between
, and whose directions of motion subtend an angle lying between  and
and
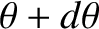 with the
with the  -axis, that cross the
-axis, that cross the  -
- plane, is
plane, is
![$\displaystyle dq_z= [\epsilon']\left[n\,F(v)\,dv\right]\left[\frac{1}{2}\,\sin\theta\,d\theta\right][v\,\cos\theta],$](img3827.png)
 is the distribution of molecular speeds, and
is the distribution of molecular speeds, and
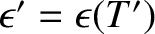 , where
, where 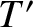 is the temperature where the molecules
last made a collision.
On average, the
molecules move a distance
is the temperature where the molecules
last made a collision.
On average, the
molecules move a distance  (i.e., the mean free path) between collisions. Hence,
(i.e., the mean free path) between collisions. Hence,
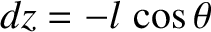 ,
and
,
and
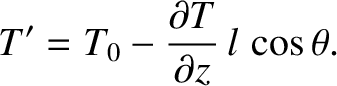
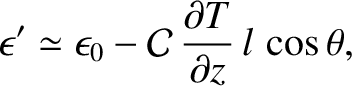
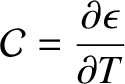
 -
- plane is
plane is
![$\displaystyle q_z =\frac{n}{2}\int_0^\pi\left[\epsilon_0-{\cal C}\,\frac{\parti...
...z}\,l\,\cos\theta\right]\cos\theta\,\sin\theta\,d\theta \int_0^\infty F(v)\,dv,$](img3833.png)
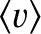 is the mean molecular speed. (See Section 5.5.9.) Thus, we conclude that the heat flux in the
is the mean molecular speed. (See Section 5.5.9.) Thus, we conclude that the heat flux in the  -direction is proportional to minus the local temperature gradient along the
-direction is proportional to minus the local temperature gradient along the  -axis. This is another example of Fick's law.
-axis. This is another example of Fick's law.

 is the molecular diameter, and
is the molecular diameter, and  the molecular mass. Moreover, for a
diatomic gas, such as air,
the molecular mass. Moreover, for a
diatomic gas, such as air,
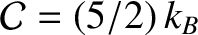 . (See Section 5.3.6.) It can be seen that the thermal conductivity of an ideal gas scales as
. (See Section 5.3.6.) It can be seen that the thermal conductivity of an ideal gas scales as 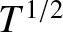 , and
is independent of the pressure at constant temperature.
The previous formula yields the following estimate for the thermal conductivity of air (assuming that
, and
is independent of the pressure at constant temperature.
The previous formula yields the following estimate for the thermal conductivity of air (assuming that
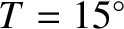 C,
C,
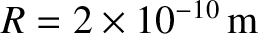 , and
, and 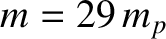 ),
),
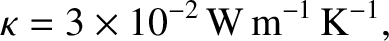
 and
and 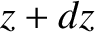 . The rate of change of the thermal energy contained in the slab is the difference between the flux of heat into the slab and the flux of
heat out of the slab. In other words,
. The rate of change of the thermal energy contained in the slab is the difference between the flux of heat into the slab and the flux of
heat out of the slab. In other words,
![$\displaystyle \frac{\partial (n\,A\,dz\,{\cal C}\,T)}{\partial t} = \left[q_z(z,t)- q_z(z+dz,t)\right]A,$](img3839.png)
 is the cross-sectional area of the slab. It follows that
is the cross-sectional area of the slab. It follows that
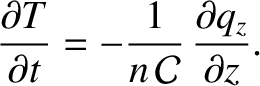
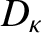 is the associated diffusivity.
Thus, we conclude, by comparison with the analysis in the previous section, that heat diffuses through
an ideal gas at the same very slow rate at which molecules diffuse. Moreover, it is clear, from Sections 5.1.5 and 5.1.7, that heat diffusion is due to a
random walk of molecules with excess energy under the action of molecular collisions.
is the associated diffusivity.
Thus, we conclude, by comparison with the analysis in the previous section, that heat diffuses through
an ideal gas at the same very slow rate at which molecules diffuse. Moreover, it is clear, from Sections 5.1.5 and 5.1.7, that heat diffusion is due to a
random walk of molecules with excess energy under the action of molecular collisions.