Suppose that an ideal gas consists of  distinct types of molecule. Let a molecule of type
distinct types of molecule. Let a molecule of type  have
a number density
have
a number density 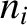 , a mass
, a mass 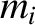 , and a velocity
, and a velocity 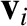 . If we repeat the analysis of Section 5.3.3, taking
into account the different types of molecule, then it is easily shown that the total pressure of the
gas is
. If we repeat the analysis of Section 5.3.3, taking
into account the different types of molecule, then it is easily shown that the total pressure of the
gas is
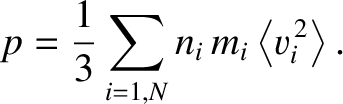 |
(5.183) |
However, the law of equipartition of energy (see the previous section) implies that
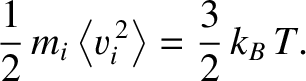 |
(5.184) |
Moreover,
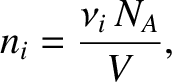 |
(5.185) |
where 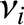 is the number of moles of molecules of type
is the number of moles of molecules of type  in the gas, and
in the gas, and  is the volume of the gas. [See Equation (5.177).] The previous three equations yield
is the volume of the gas. [See Equation (5.177).] The previous three equations yield
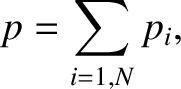 |
(5.186) |
where
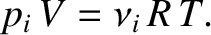 |
(5.187) |
We conclude that the total pressure of the gas is the sum of the pressures that a gas of each constituent type of molecule would
exert independently. This result is known as Dalton's law, after John Dalton, who verified it experimentally
in 1802. The quantity  is known as the partial pressure of type-
is known as the partial pressure of type- molecules. Thus,
Dalton's law is equivalent to the statement that the total pressure of an ideal gas is the sum of the partial pressures
of the individual gases from which it is composed.
molecules. Thus,
Dalton's law is equivalent to the statement that the total pressure of an ideal gas is the sum of the partial pressures
of the individual gases from which it is composed.
 distinct types of molecule. Let a molecule of type
distinct types of molecule. Let a molecule of type  have
a number density
have
a number density 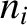 , a mass
, a mass 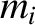 , and a velocity
, and a velocity 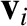 . If we repeat the analysis of Section 5.3.3, taking
into account the different types of molecule, then it is easily shown that the total pressure of the
gas is
. If we repeat the analysis of Section 5.3.3, taking
into account the different types of molecule, then it is easily shown that the total pressure of the
gas is
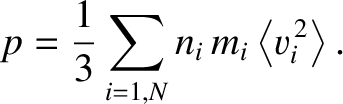
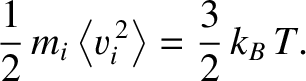
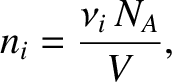
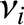 is the number of moles of molecules of type
is the number of moles of molecules of type  in the gas, and
in the gas, and  is the volume of the gas. [See Equation (5.177).] The previous three equations yield
is the volume of the gas. [See Equation (5.177).] The previous three equations yield
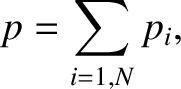
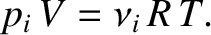
 is known as the partial pressure of type-
is known as the partial pressure of type- molecules. Thus,
Dalton's law is equivalent to the statement that the total pressure of an ideal gas is the sum of the partial pressures
of the individual gases from which it is composed.
molecules. Thus,
Dalton's law is equivalent to the statement that the total pressure of an ideal gas is the sum of the partial pressures
of the individual gases from which it is composed.