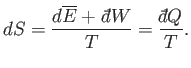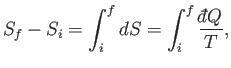Next: Entropy
Up: Statistical Thermodynamics
Previous: Mechanical Interaction Between Macrosystems
General Interaction Between Macrosystems
Consider two systems,  and
and  , that can interact by exchanging heat energy
and
doing work on one another. Let the system
, that can interact by exchanging heat energy
and
doing work on one another. Let the system  have energy
have energy  , and adjustable external
parameters
, and adjustable external
parameters
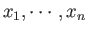 . Likewise, let the
system
. Likewise, let the
system  have energy
have energy 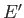 , and adjustable
external parameters
, and adjustable
external parameters
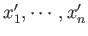 . The combined system
. The combined system
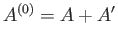 is
assumed to be isolated. It follows from the first law of thermodynamics that
is
assumed to be isolated. It follows from the first law of thermodynamics that
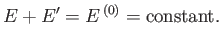 |
(5.42) |
Thus, the energy 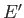 of system
of system  is determined once the energy
is determined once the energy  of
system
of
system  is given, and vice versa. In fact,
is given, and vice versa. In fact, 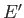 could be regarded as
a function of
could be regarded as
a function of  . Furthermore, if the two systems can interact mechanically then,
in general, the parameters
. Furthermore, if the two systems can interact mechanically then,
in general, the parameters 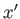 are some function of the parameters
are some function of the parameters  . As
a simple example, if the two systems are separated by a movable partition, in
an enclosure of fixed volume
. As
a simple example, if the two systems are separated by a movable partition, in
an enclosure of fixed volume 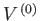 , then
, then
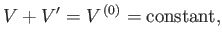 |
(5.43) |
where  and
and 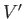 are the volumes of systems
are the volumes of systems  and
and  , respectively.
, respectively.
The total number of microstates accessible to 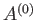 is clearly a function of
is clearly a function of
 , and the parameters
, and the parameters  (where
(where 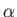 runs from 1 to
runs from 1 to  ), so
), so
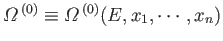 .
We have already demonstrated (in
Section 5.2) that
.
We have already demonstrated (in
Section 5.2) that
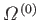 exhibits a very pronounced maximum at one particular
value of the energy,
exhibits a very pronounced maximum at one particular
value of the energy,
 , when
, when  is varied but the external parameters are held constant.
This behavior comes about because of the very strong,
is varied but the external parameters are held constant.
This behavior comes about because of the very strong,
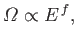 |
(5.44) |
increase in the number of accessible microstates of  (or
(or  )
with energy. However, according to Section 3.8, the number of
accessible microstates exhibits a similar strong increase with
the volume, which is a typical external parameter, so that
)
with energy. However, according to Section 3.8, the number of
accessible microstates exhibits a similar strong increase with
the volume, which is a typical external parameter, so that
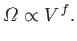 |
(5.45) |
It follows that the variation of
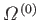 with a typical parameter,
with a typical parameter,  ,
when all the other parameters and the energy are held constant, also exhibits
a very
sharp maximum at some particular
value,
,
when all the other parameters and the energy are held constant, also exhibits
a very
sharp maximum at some particular
value,
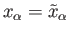 . The equilibrium situation
corresponds to the configuration of maximum probability, in which virtually all
systems
. The equilibrium situation
corresponds to the configuration of maximum probability, in which virtually all
systems  in the ensemble have values of
in the ensemble have values of  and
and  very close
to
very close
to 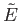 and
and
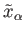 , respectively. The mean values of these quantities are
thus given by
, respectively. The mean values of these quantities are
thus given by
 and
and
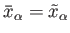 .
.
Consider a quasi-static process in which the system  is brought from an equilibrium
state described by
is brought from an equilibrium
state described by
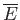 and
and
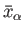 to an infinitesimally different
equilibrium state described by
to an infinitesimally different
equilibrium state described by
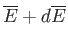 and
and
 . Let us calculate the resultant change in the
number of microstates accessible to
. Let us calculate the resultant change in the
number of microstates accessible to  . Because
. Because
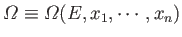 , the change in
, the change in
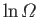 follows from standard mathematics:
follows from standard mathematics:
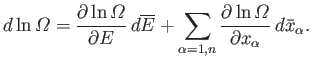 |
(5.46) |
However, we have previously demonstrated that
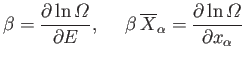 |
(5.47) |
[in Equations (5.30) and (5.41), respectively],
so Equation (5.46) can be written
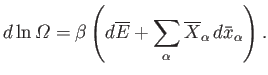 |
(5.48) |
Note that the temperature parameter, 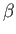 , and the mean conjugate forces,
, and the mean conjugate forces,
 , are only well defined for equilibrium states. This is
why we are only considering quasi-static changes
in which the two systems are always
arbitrarily close to equilibrium.
, are only well defined for equilibrium states. This is
why we are only considering quasi-static changes
in which the two systems are always
arbitrarily close to equilibrium.
Let us rewrite Equation (5.48)
in terms of the thermodynamic temperature,  ,
using the relation
,
using the relation
 . We obtain
. We obtain
 |
(5.49) |
where
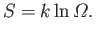 |
(5.50) |
Equation (5.49) is a differential relation that enables us to calculate
the quantity
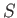 as a function of the mean energy,
as a function of the mean energy,
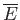 , and the mean external parameters,
, and the mean external parameters,
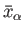 , assuming that we can calculate the temperature,
, assuming that we can calculate the temperature,  , and mean
conjugate forces,
, and mean
conjugate forces,
 , for each equilibrium state. The function
, for each equilibrium state. The function
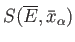 is termed the entropy of system
is termed the entropy of system  . The word
entropy is derived from the Greek entrope, which means ``a turning towards" or "tendency."
The reason for this etymology
will become apparent presently. It can be seen from Equation (5.50)
that the entropy is merely a parameterization
of the number of accessible microstates.
Hence, according to statistical mechanics,
. The word
entropy is derived from the Greek entrope, which means ``a turning towards" or "tendency."
The reason for this etymology
will become apparent presently. It can be seen from Equation (5.50)
that the entropy is merely a parameterization
of the number of accessible microstates.
Hence, according to statistical mechanics,
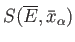 is essentially
a measure of the relative probability
of a state characterized by values of the mean energy and mean external parameters
is essentially
a measure of the relative probability
of a state characterized by values of the mean energy and mean external parameters
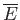 and
and
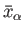 , respectively.
, respectively.
According to Equation (4.16), the net amount of work performed during a quasi-static
change is given by
 |
(5.51) |
It follows from Equation (5.49) that
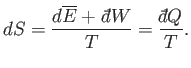 |
(5.52) |
Thus, the thermodynamic temperature,  , is the integrating factor for the
first law of thermodynamics,
, is the integrating factor for the
first law of thermodynamics,
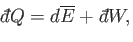 |
(5.53) |
which converts the inexact differential
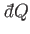 into the exact
differential
into the exact
differential 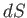 . (See Section 4.5.)
It follows that the entropy difference between any two macrostates
. (See Section 4.5.)
It follows that the entropy difference between any two macrostates
 and
and 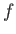 can be written
can be written
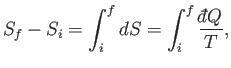 |
(5.54) |
where the integral is evaluated for any process through which the system is brought
quasi-statically via a sequence of near-equilibrium configurations
from its initial to its final macrostate. The process has to be quasi-static
because the temperature,  , which appears in the integrand, is only well defined
for an equilibrium state. Because the left-hand side of the previous equation only depends
on the initial and final states, it follows that the integral on the right-hand side
is independent of the particular sequence of quasi-static changes used to get
from
, which appears in the integrand, is only well defined
for an equilibrium state. Because the left-hand side of the previous equation only depends
on the initial and final states, it follows that the integral on the right-hand side
is independent of the particular sequence of quasi-static changes used to get
from  to
to 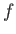 . Thus,
. Thus,
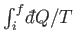 is independent of the
process (provided that it is quasi-static).
is independent of the
process (provided that it is quasi-static).
All of the concepts that we have encountered up to now in this course, such
as temperature, heat, energy, volume, pressure, et cetera, have been fairly
familiar to us
from other branches of physics.
However, entropy, which turns out to be of crucial importance
in thermodynamics, is something quite new. Let us consider the following
questions. What does the entropy of a thermodynamic system actually signify? What use is
the concept of entropy?



Next: Entropy
Up: Statistical Thermodynamics
Previous: Mechanical Interaction Between Macrosystems
Richard Fitzpatrick
2016-01-25
![]() is clearly a function of
is clearly a function of
![]() , and the parameters
, and the parameters ![]() (where
(where ![]() runs from 1 to
runs from 1 to ![]() ), so
), so
![]() .
We have already demonstrated (in
Section 5.2) that
.
We have already demonstrated (in
Section 5.2) that
![]() exhibits a very pronounced maximum at one particular
value of the energy,
exhibits a very pronounced maximum at one particular
value of the energy,
![]() , when
, when ![]() is varied but the external parameters are held constant.
This behavior comes about because of the very strong,
is varied but the external parameters are held constant.
This behavior comes about because of the very strong,
![]() is brought from an equilibrium
state described by
is brought from an equilibrium
state described by
![]() and
and
![]() to an infinitesimally different
equilibrium state described by
to an infinitesimally different
equilibrium state described by
![]() and
and
![]() . Let us calculate the resultant change in the
number of microstates accessible to
. Let us calculate the resultant change in the
number of microstates accessible to ![]() . Because
. Because
![]() , the change in
, the change in
![]() follows from standard mathematics:
follows from standard mathematics:
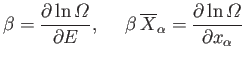
![]() ,
using the relation
,
using the relation
![]() . We obtain
. We obtain