


Next: General Interaction Between Macrosystems
Up: Statistical Thermodynamics
Previous: Temperature
Let us now examine a purely mechanical interaction between macrostates, where one
or more of the external parameters is modified, but there is no exchange of
heat energy. Consider, for the sake of simplicity, a situation where only
one external parameter,  , of the system is free to vary.
In general, the number of microstates
accessible to the system when the overall energy lies between
, of the system is free to vary.
In general, the number of microstates
accessible to the system when the overall energy lies between  and
and
 depends on the particular value of
depends on the particular value of  , so we can write
, so we can write
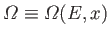 .
.
When  is changed by the amount
is changed by the amount 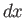 , the energy
, the energy 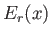 of a given
microstate
of a given
microstate
 changes by
changes by
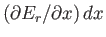 . The number of states,
. The number of states,
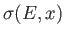 , whose energy is changed from a value less than
, whose energy is changed from a value less than  to a value
greater than
to a value
greater than  , when the parameter changes from
, when the parameter changes from  to
to 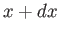 , is given by
the number of microstates per unit energy range multiplied by the average
shift in energy of the microstates. Hence,
, is given by
the number of microstates per unit energy range multiplied by the average
shift in energy of the microstates. Hence,
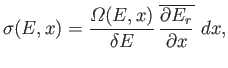 |
(5.34) |
where the mean value of
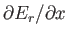 is taken over all accessible
microstates (i.e., all states for which the energy lies between
is taken over all accessible
microstates (i.e., all states for which the energy lies between  and
and
 , and
the external parameter takes the value
, and
the external parameter takes the value  ). The previous equation can also be written
). The previous equation can also be written
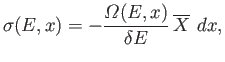 |
(5.35) |
where
 |
(5.36) |
is the mean generalized force conjugate to the external parameter  .
(See Section 4.4.)
.
(See Section 4.4.)
Consider the total number of microstates whose energies lies between  and
and
 . When the
external parameter changes from
. When the
external parameter changes from  to
to 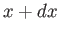 , the number of states in this energy
range changes by
, the number of states in this energy
range changes by
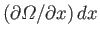 . This change is
due to the difference between the number of states that enter the
range because their energy is changed from a value less than
. This change is
due to the difference between the number of states that enter the
range because their energy is changed from a value less than  to one greater than
to one greater than
 , and the number that
leave
because their energy is changed from a value less than
, and the number that
leave
because their energy is changed from a value less than
 to one
greater than
to one
greater than
 .
In symbols,
.
In symbols,
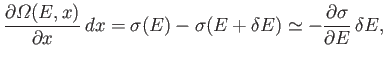 |
(5.37) |
which yields
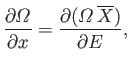 |
(5.38) |
where use has been made of Equation (5.35). Dividing both sides by
 gives
gives
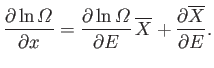 |
(5.39) |
However, according to the usual estimate
 (see Section 3.8), the first term on the
right-hand side is of order
(see Section 3.8), the first term on the
right-hand side is of order
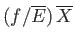 , whereas the second term is only
of order
, whereas the second term is only
of order
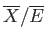 .
Clearly, for a macroscopic system with many degrees of freedom,
the second term is utterly negligible, so we have
.
Clearly, for a macroscopic system with many degrees of freedom,
the second term is utterly negligible, so we have
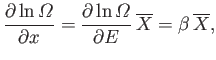 |
(5.40) |
where use has been made of Equation (5.30).
When there are several external parameters,
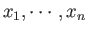 , so that
, so that
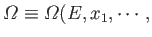
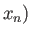 , the previous derivation is valid for
each parameter
taken in isolation. Thus,
, the previous derivation is valid for
each parameter
taken in isolation. Thus,
 |
(5.41) |
where
 is the mean generalized force conjugate to the parameter
is the mean generalized force conjugate to the parameter
 . (See Section B.2.)
. (See Section B.2.)



Next: General Interaction Between Macrosystems
Up: Statistical Thermodynamics
Previous: Temperature
Richard Fitzpatrick
2016-01-25
![]() is changed by the amount
is changed by the amount ![]() , the energy
, the energy ![]() of a given
microstate
of a given
microstate
![]() changes by
changes by
![]() . The number of states,
. The number of states,
![]() , whose energy is changed from a value less than
, whose energy is changed from a value less than ![]() to a value
greater than
to a value
greater than ![]() , when the parameter changes from
, when the parameter changes from ![]() to
to ![]() , is given by
the number of microstates per unit energy range multiplied by the average
shift in energy of the microstates. Hence,
, is given by
the number of microstates per unit energy range multiplied by the average
shift in energy of the microstates. Hence,
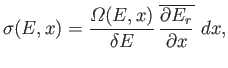

![]() and
and
![]() . When the
external parameter changes from
. When the
external parameter changes from ![]() to
to ![]() , the number of states in this energy
range changes by
, the number of states in this energy
range changes by
![]() . This change is
due to the difference between the number of states that enter the
range because their energy is changed from a value less than
. This change is
due to the difference between the number of states that enter the
range because their energy is changed from a value less than ![]() to one greater than
to one greater than
![]() , and the number that
leave
because their energy is changed from a value less than
, and the number that
leave
because their energy is changed from a value less than
![]() to one
greater than
to one
greater than
![]() .
In symbols,
.
In symbols,
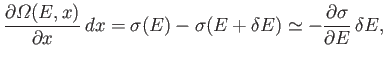
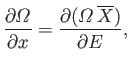
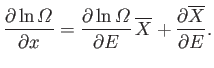
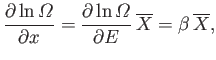
![]() , so that
, so that
![]()
![]() , the previous derivation is valid for
each parameter
taken in isolation. Thus,
, the previous derivation is valid for
each parameter
taken in isolation. Thus,