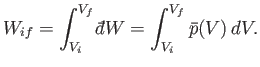Next: Exact and Inexact Differentials
Up: Heat and Work
Previous: Microscopic Interpretation of Heat
Quasi-Static Processes
Consider the special case of an interaction of the system  with its surroundings
that is carried out so slowly that
with its surroundings
that is carried out so slowly that  remains arbitrarily close to equilibrium
at all times. Such a process is said to be quasi-static for
the system
remains arbitrarily close to equilibrium
at all times. Such a process is said to be quasi-static for
the system  . In practice, a quasi-static process must be carried out on
a timescale that is much longer than the relaxation time of the system.
Recall
that the relaxation time is the typical timescale for the system to return
to equilibrium after being suddenly disturbed. (See Section 3.5.)
. In practice, a quasi-static process must be carried out on
a timescale that is much longer than the relaxation time of the system.
Recall
that the relaxation time is the typical timescale for the system to return
to equilibrium after being suddenly disturbed. (See Section 3.5.)
A finite quasi-static change can be built up out of many infinitesimal changes.
The infinitesimal heat,
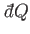 , absorbed by the system when infinitesimal work,
, absorbed by the system when infinitesimal work,
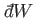 , is done on its environment,
and its average energy changes by
, is done on its environment,
and its average energy changes by
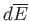 , is
given by
, is
given by
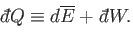 |
(4.11) |
The special symbols
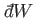 and
and
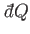 are introduced to emphasize that the
work done, and the heat absorbed, are infinitesimal quantities that
do not correspond to the
difference between two works or two heats. Instead, the work done, and the heat absorbed,
depend on the interaction process itself. Thus, it makes no sense to talk
about the work in the system before and after the process, or the difference between
these.
are introduced to emphasize that the
work done, and the heat absorbed, are infinitesimal quantities that
do not correspond to the
difference between two works or two heats. Instead, the work done, and the heat absorbed,
depend on the interaction process itself. Thus, it makes no sense to talk
about the work in the system before and after the process, or the difference between
these.
If the external parameters of the system have the values 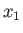 ,
,
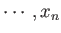 then
the energy of the system in a definite microstate,
then
the energy of the system in a definite microstate, 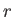 , can be written
, can be written
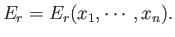 |
(4.12) |
Hence, if the external parameters are changed by infinitesimal amounts, so that
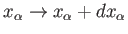 for
for 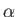 in the range 1 to
in the range 1 to 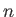 , then
the corresponding change in the energy of the microstate is
, then
the corresponding change in the energy of the microstate is
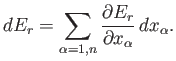 |
(4.13) |
The work,
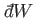 , done by the system when it remains in this particular
state
, done by the system when it remains in this particular
state 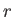 is [see Equation (4.8)]
is [see Equation (4.8)]
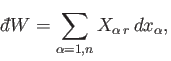 |
(4.14) |
where
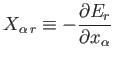 |
(4.15) |
is termed the generalized force (conjugate to the external parameter 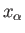 )
in the state
)
in the state 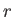 . (See Section B.2.) Note that if
. (See Section B.2.) Note that if 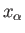 is a displacement then
is a displacement then
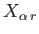 is
an ordinary force.
is
an ordinary force.
Consider, now, an ensemble of systems. Provided that the external
parameters of the system are changed quasi-statically, the generalized forces
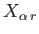 have well-defined mean values that are calculable from the
distribution of systems in the ensemble characteristic of the instantaneous
macrostate.
The macroscopic work,
have well-defined mean values that are calculable from the
distribution of systems in the ensemble characteristic of the instantaneous
macrostate.
The macroscopic work,
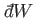 , resulting
from an infinitesimal quasi-static change of the external parameters is obtained by
calculating the decrease in the mean energy resulting from the parameter change.
Thus,
, resulting
from an infinitesimal quasi-static change of the external parameters is obtained by
calculating the decrease in the mean energy resulting from the parameter change.
Thus,
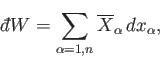 |
(4.16) |
where
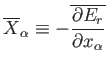 |
(4.17) |
is the mean generalized force conjugate to 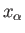 . The mean value is
calculated from the equilibrium distribution of systems in the ensemble corresponding to the external parameter values
. The mean value is
calculated from the equilibrium distribution of systems in the ensemble corresponding to the external parameter values 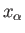 . The macroscopic work,
. The macroscopic work, 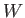 , resulting
from a finite quasi-static change of external parameters can be obtained by
integrating Equation (4.16).
, resulting
from a finite quasi-static change of external parameters can be obtained by
integrating Equation (4.16).
The most well-known example of quasi-static work in thermodynamics is that done by
pressure when the volume changes. For simplicity, suppose that the
volume  is the only external parameter of any consequence. The work done in
changing the volume from
is the only external parameter of any consequence. The work done in
changing the volume from  to
to 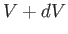 is simply the product of the force and
the displacement (along the line of action of the force). By definition, the mean
equilibrium pressure,
is simply the product of the force and
the displacement (along the line of action of the force). By definition, the mean
equilibrium pressure, 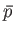 ,
of a given macrostate is equal to the normal force per unit area acting
on any surface element. Thus, the normal force acting on a surface element
,
of a given macrostate is equal to the normal force per unit area acting
on any surface element. Thus, the normal force acting on a surface element
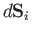 is
is
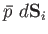 . Suppose that the surface element is subject
to a
displacement
. Suppose that the surface element is subject
to a
displacement
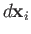 . The work done by the element is
. The work done by the element is
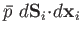 .
The total work done by the system is obtained by summing over all of the surface
elements. Thus,
.
The total work done by the system is obtained by summing over all of the surface
elements. Thus,
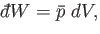 |
(4.18) |
where
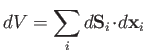 |
(4.19) |
is the infinitesimal volume change due to the displacement of the surface.
It follows from Equations (4.16) and (4.18) that
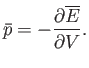 |
(4.20) |
Thus, the mean pressure is the generalized force conjugate to the volume,  .
.
Suppose that a quasi-static process is carried out in which the volume is changed
from 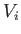 to
to 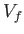 . In general, the mean pressure,
. In general, the mean pressure, 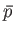 , is a function of the volume, so
, is a function of the volume, so
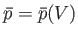 . It follows that the macroscopic work done by the
system is given by
. It follows that the macroscopic work done by the
system is given by
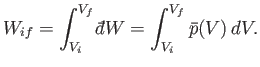 |
(4.21) |
This quantity is just the area under the curve in a plot of
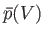 versus
versus
 .
.



Next: Exact and Inexact Differentials
Up: Heat and Work
Previous: Microscopic Interpretation of Heat
Richard Fitzpatrick
2016-01-25
![]() , absorbed by the system when infinitesimal work,
, absorbed by the system when infinitesimal work,
![]() , is done on its environment,
and its average energy changes by
, is done on its environment,
and its average energy changes by
![]() , is
given by
, is
given by
![]() ,
,
![]() then
the energy of the system in a definite microstate,
then
the energy of the system in a definite microstate, ![]() , can be written
, can be written
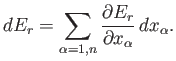
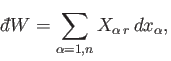
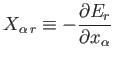
![]() have well-defined mean values that are calculable from the
distribution of systems in the ensemble characteristic of the instantaneous
macrostate.
The macroscopic work,
have well-defined mean values that are calculable from the
distribution of systems in the ensemble characteristic of the instantaneous
macrostate.
The macroscopic work,
![]() , resulting
from an infinitesimal quasi-static change of the external parameters is obtained by
calculating the decrease in the mean energy resulting from the parameter change.
Thus,
, resulting
from an infinitesimal quasi-static change of the external parameters is obtained by
calculating the decrease in the mean energy resulting from the parameter change.
Thus,
![]() is the only external parameter of any consequence. The work done in
changing the volume from
is the only external parameter of any consequence. The work done in
changing the volume from ![]() to
to ![]() is simply the product of the force and
the displacement (along the line of action of the force). By definition, the mean
equilibrium pressure,
is simply the product of the force and
the displacement (along the line of action of the force). By definition, the mean
equilibrium pressure, ![]() ,
of a given macrostate is equal to the normal force per unit area acting
on any surface element. Thus, the normal force acting on a surface element
,
of a given macrostate is equal to the normal force per unit area acting
on any surface element. Thus, the normal force acting on a surface element
![]() is
is
![]() . Suppose that the surface element is subject
to a
displacement
. Suppose that the surface element is subject
to a
displacement
![]() . The work done by the element is
. The work done by the element is
![]() .
The total work done by the system is obtained by summing over all of the surface
elements. Thus,
.
The total work done by the system is obtained by summing over all of the surface
elements. Thus,
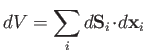
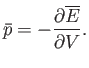
![]() to
to ![]() . In general, the mean pressure,
. In general, the mean pressure, ![]() , is a function of the volume, so
, is a function of the volume, so
![]() . It follows that the macroscopic work done by the
system is given by
. It follows that the macroscopic work done by the
system is given by