


Next: Quasi-Static Processes
Up: Heat and Work
Previous: Macrostates and Microstates
Consider a macroscopic system,  , that is
known to be in a given macrostate. To be more exact,
consider an ensemble
of similar macroscopic systems,
, that is
known to be in a given macrostate. To be more exact,
consider an ensemble
of similar macroscopic systems,  , where each system in the ensemble
is in one of the many microstates consistent with the given
macrostate. There are two fundamentally different ways
in which the average energy of
, where each system in the ensemble
is in one of the many microstates consistent with the given
macrostate. There are two fundamentally different ways
in which the average energy of  can change due to interaction with its
surroundings. If the external parameters of the system remain constant then the
interaction is termed a purely thermal interaction. Any change in the average
energy of the system is attributed to an exchange of heat with its environment.
Thus,
can change due to interaction with its
surroundings. If the external parameters of the system remain constant then the
interaction is termed a purely thermal interaction. Any change in the average
energy of the system is attributed to an exchange of heat with its environment.
Thus,
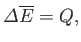 |
(4.7) |
where 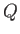 is the heat absorbed by the system. On a microscopic level, the
energies of the individual microstates are unaffected by the absorption of heat.
In fact, it is the distribution of the systems in the ensemble
over the various microstates that is modified.
is the heat absorbed by the system. On a microscopic level, the
energies of the individual microstates are unaffected by the absorption of heat.
In fact, it is the distribution of the systems in the ensemble
over the various microstates that is modified.
Suppose that the system  is thermally insulated from its environment. This can be
achieved by surrounding it by an adiabatic envelope (i.e., an envelope
fabricated out of a material that is a poor conductor of heat, such a fiber glass).
Incidentally, the term adiabatic is derived from the Greek adiabatos, which
means ``impassable.'' In scientific terminology, an adiabatic process is one in
which there is no exchange of heat. The system
is thermally insulated from its environment. This can be
achieved by surrounding it by an adiabatic envelope (i.e., an envelope
fabricated out of a material that is a poor conductor of heat, such a fiber glass).
Incidentally, the term adiabatic is derived from the Greek adiabatos, which
means ``impassable.'' In scientific terminology, an adiabatic process is one in
which there is no exchange of heat. The system  is still capable of interacting
with its environment via its external parameters. This type of interaction is
termed mechanical interaction, and any change in the average energy of the
system is attributed to work done on it by its surroundings. Thus,
is still capable of interacting
with its environment via its external parameters. This type of interaction is
termed mechanical interaction, and any change in the average energy of the
system is attributed to work done on it by its surroundings. Thus,
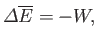 |
(4.8) |
where 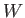 is the work done by the system on its environment. On a microscopic level,
the energy of the
system changes because the energies of the individual microstates are
functions of the external parameters. [See Equation (4.6).]
Thus, if the external parameters
are changed then, in general, the energies of all of the systems in the ensemble
are modified (because each is in a specific microstate). Such a modification
usually gives rise to a redistribution of the systems in the ensemble over the
accessible microstates (without any heat
exchange with the environment). Clearly, from a microscopic viewpoint, performing
work on
a macroscopic system is quite a complicated process. Nevertheless, macroscopic work
is a quantity that is easy to measure experimentally. For instance, if
the system
is the work done by the system on its environment. On a microscopic level,
the energy of the
system changes because the energies of the individual microstates are
functions of the external parameters. [See Equation (4.6).]
Thus, if the external parameters
are changed then, in general, the energies of all of the systems in the ensemble
are modified (because each is in a specific microstate). Such a modification
usually gives rise to a redistribution of the systems in the ensemble over the
accessible microstates (without any heat
exchange with the environment). Clearly, from a microscopic viewpoint, performing
work on
a macroscopic system is quite a complicated process. Nevertheless, macroscopic work
is a quantity that is easy to measure experimentally. For instance, if
the system  exerts a force
exerts a force 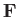 on its immediate surroundings, and
the change in external parameters corresponds to a displacement
on its immediate surroundings, and
the change in external parameters corresponds to a displacement 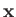 of the center of mass of the system, then the work done by
of the center of mass of the system, then the work done by
 on its surroundings
is simply
on its surroundings
is simply
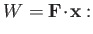 |
(4.9) |
that is, the product of the force and the displacement along the line of action
of the force.
In a general interaction of the system  with its environment there is both
heat exchange and work performed. We can write
with its environment there is both
heat exchange and work performed. We can write
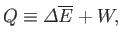 |
(4.10) |
which serves as the general definition of the absorbed heat 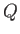 . (Hence, the
equivalence sign.) The quantity
. (Hence, the
equivalence sign.) The quantity 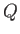 is
simply the change in the mean energy of the system
that is not due to the modification of the
external parameters. Note that the notion of a quantity of heat has no independent
meaning apart from Equation (4.10). The mean energy,
is
simply the change in the mean energy of the system
that is not due to the modification of the
external parameters. Note that the notion of a quantity of heat has no independent
meaning apart from Equation (4.10). The mean energy,
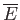 , and work
performed,
, and work
performed, 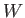 , are
both physical quantities that can be determined experimentally, whereas
, are
both physical quantities that can be determined experimentally, whereas
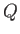 is merely a derived quantity.
is merely a derived quantity.



Next: Quasi-Static Processes
Up: Heat and Work
Previous: Macrostates and Microstates
Richard Fitzpatrick
2016-01-25
![]() is thermally insulated from its environment. This can be
achieved by surrounding it by an adiabatic envelope (i.e., an envelope
fabricated out of a material that is a poor conductor of heat, such a fiber glass).
Incidentally, the term adiabatic is derived from the Greek adiabatos, which
means ``impassable.'' In scientific terminology, an adiabatic process is one in
which there is no exchange of heat. The system
is thermally insulated from its environment. This can be
achieved by surrounding it by an adiabatic envelope (i.e., an envelope
fabricated out of a material that is a poor conductor of heat, such a fiber glass).
Incidentally, the term adiabatic is derived from the Greek adiabatos, which
means ``impassable.'' In scientific terminology, an adiabatic process is one in
which there is no exchange of heat. The system ![]() is still capable of interacting
with its environment via its external parameters. This type of interaction is
termed mechanical interaction, and any change in the average energy of the
system is attributed to work done on it by its surroundings. Thus,
is still capable of interacting
with its environment via its external parameters. This type of interaction is
termed mechanical interaction, and any change in the average energy of the
system is attributed to work done on it by its surroundings. Thus,