Next: Electromagnetic Torques Up: Cylindrical Tearing Mode Theory Previous: Resistive Layer Physics Contents
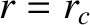 is replaced by a radially-thin, magnetic field-coil that carries a
helical current possessing
is replaced by a radially-thin, magnetic field-coil that carries a
helical current possessing  periods in the poloidal direction, and
periods in the poloidal direction, and 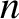 periods in the toroidal direction. Let the current density in the field-coil
take the form
where
periods in the toroidal direction. Let the current density in the field-coil
take the form
where
 .
Here, the complex quantity
.
Here, the complex quantity 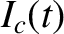 specifies the amplitude and phase of the helical current flowing in the field-coil.
Note that
specifies the amplitude and phase of the helical current flowing in the field-coil.
Note that
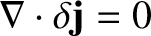 , as is required by charge conservation.
, as is required by charge conservation.
The most general solution to the cylindrical tearing mode equation, (3.60), in the outer region can now be written
where the real functions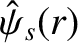 and
and
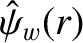 are specified in Sections 3.8 and 3.9, respectively.
Moreover,
the real function
are specified in Sections 3.8 and 3.9, respectively.
Moreover,
the real function
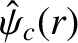 is a solution of
that satisfies
is a solution of
that satisfies
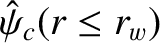 |
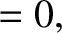 |
(3.114) |
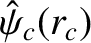 |
 |
(3.115) |
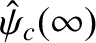 |
 |
(3.116) |
In general,
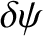 is continuous across the field-coil (in accordance with Maxwell's equations), whereas
is continuous across the field-coil (in accordance with Maxwell's equations), whereas
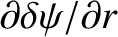 is discontinuous. The discontinuity in
is discontinuous. The discontinuity in
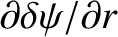 is caused by the helical current flowing in the field-coil. The complex quantity
is caused by the helical current flowing in the field-coil. The complex quantity
Simultaneously matching the outer solution, (3.112), across the rational surface, the resistive wall, and the field-coil, we obtain
Here, where use has been made of Equations (3.81), (3.118), and (3.119).