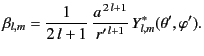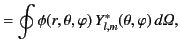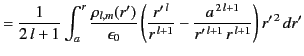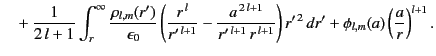Next: Newmann Problem in Spherical
Up: Potential Theory
Previous: Axisymmetric Charge Distributions
We saw in Section 2.10 that the solution to the Dirichlet problem, in which the charge density is specified
within some volume  , and the potential given on the bounding surface
, and the potential given on the bounding surface  ,
takes the form
,
takes the form
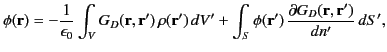 |
(371) |
where the Dirichlet Green's function is
written
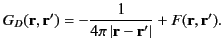 |
(372) |
Here,
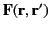 is solution of Laplace's equation (i.e.,
is solution of Laplace's equation (i.e.,
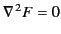 ) which is chosen so as to ensure that
) which is chosen so as to ensure that
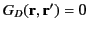 when
when  (or
(or  ) lies on
) lies on  . Thus, it follows from Sections 3.4 and 3.5
that
. Thus, it follows from Sections 3.4 and 3.5
that
where the
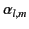 and the
and the
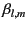 are chosen in such a manner that the Green's function is zero when
are chosen in such a manner that the Green's function is zero when  lies on
lies on  .
.
As a specific example, suppose that the volume  lies between the two spherical surfaces
lies between the two spherical surfaces  and
and  .
The constraint that
.
The constraint that
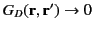 as
as
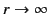 implies that the
implies that the
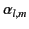 are all zero.
On the other hand, the constraint
are all zero.
On the other hand, the constraint
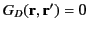 when
when  yields
yields
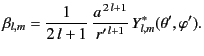 |
(374) |
Hence, the unique Green's function for the problem becomes
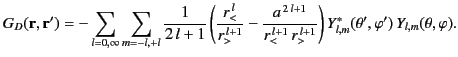 |
(375) |
Furthermore, it is readily demonstrated that
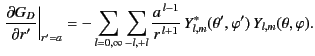 |
(376) |
It is convenient to write
It follows from Equation (311) that
Thus, Equations (372), (376) and
(377) yield



Next: Newmann Problem in Spherical
Up: Potential Theory
Previous: Axisymmetric Charge Distributions
Richard Fitzpatrick
2014-06-27
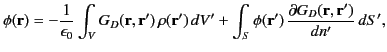
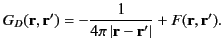
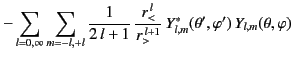
![$\displaystyle + \sum_{l=0,\infty}\sum_{m=-l,+l}\left[\alpha_{l,m}(r',\theta',\v...
...rac{\beta_{l,m}(r',\theta',\varphi')}{r^{\,l+1}}\right]Y_{l,m}(\theta,\varphi),$](img834.png)
![]() lies between the two spherical surfaces
lies between the two spherical surfaces ![]() and
and ![]() .
The constraint that
.
The constraint that
![]() as
as
![]() implies that the
implies that the
![]() are all zero.
On the other hand, the constraint
are all zero.
On the other hand, the constraint
![]() when
when ![]() yields
yields