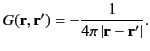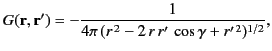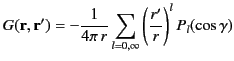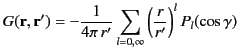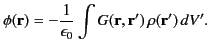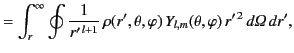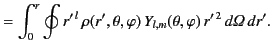Next: Multipole Expansion
Up: Potential Theory
Previous: Laplace's Equation in Spherical
Poisson's Equation in Spherical Coordinates
Consider the general solution to Poisson's equation,
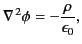 |
(328) |
in spherical coordinates.
According to Section 2.3, the general three-dimensional Green's function for Poisson's equation is
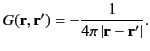 |
(329) |
When expressed in terms of spherical coordinates, this becomes
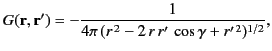 |
(330) |
where
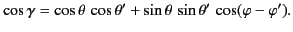 |
(331) |
is the angle subtended between 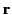 and
and 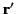 . According to Equation (298), we can write
. According to Equation (298), we can write
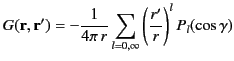 |
(332) |
for 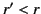 , and
, and
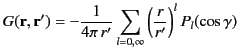 |
(333) |
for 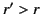 . Thus, it follows from the spherical harmonic addition theorem, (322), that
. Thus, it follows from the spherical harmonic addition theorem, (322), that
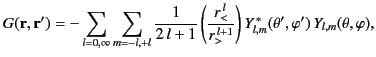 |
(334) |
where 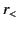 represents the lesser of
represents the lesser of 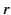 and
and 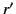 , whereas
, whereas 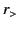 represents the greater of
represents the greater of 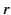 and
and 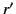 .
.
According to Section 2.3, the general solution to Poisson's equation, (329), is
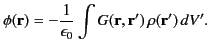 |
(335) |
Thus, Equation (335) yields
![$\displaystyle \phi({\bf r}) = \frac{1}{\epsilon_0}\sum_{l=0,\infty}\sum_{m=-l,+...
...,\ast}(r)+ \frac{q_{l,m}^{\,\ast}(r)}{r^{\,l+1}}\right]Y_{l,m}(\theta,\varphi),$](img753.png) |
(336) |
where



Next: Multipole Expansion
Up: Potential Theory
Previous: Laplace's Equation in Spherical
Richard Fitzpatrick
2014-06-27