Next: Poisson's Equation in Spherical Up: Potential Theory Previous: Spherical Harmonics

Laplace's Equation in Spherical Coordinates

Consider the general solution to Laplace's equation,

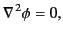$\displaystyle \nabla^{\,2}\phi = 0,$

(322)

in spherical coordinates. Let us write

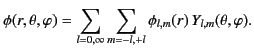$\displaystyle \phi(r,\theta,\varphi) = \sum_{l=0,\infty}\sum_{m=-l,+l}\phi_{l,m}(r)\,Y_{l,m}(\theta,\varphi).$

(323)

It follows from Equation (308) that

$\displaystyle \sum_{l=0,\infty}\sum_{m=-l,+l}\left[\frac{d}{dr}\!\left(r^{\,2}\... ...c{d\phi_{l,m}}{dr}\right)-l\,(l+1)\,\phi_{l,m}\right]Y_{l,m}(\theta,\varphi)=0.$

(324)

However, given that the spherical harmonics are mutually orthogonal [in the sense that they satisfy Equation (311)], we can separately equate the coefficients of each in the above equation, to give

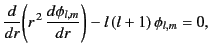$\displaystyle \frac{d}{dr}\!\left(r^{\,2}\,\frac{d\phi_{l,m}}{dr}\right)-l\,(l+1)\,\phi_{l,m}=0,$

(325)

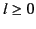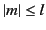for all $l\geq 0$ and $\vert m\vert\leq l$ . It follows that

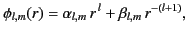$\displaystyle \phi_{l,m}(r)=\alpha_{l,m}\,r^{\,l} + \beta_{l,m}\,r^{-(l+1)},$

(326)

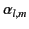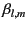where the $\alpha_{l,m}$ and $\beta_{l,m}$ are arbitrary constants. Hence, the general solution to Laplace's equation in spherical coordinates is written

$\displaystyle \phi(r,\theta,\varphi)= \sum_{l=0,\infty}\sum_{m=-l,+l}\left[\alpha_{l,m}\,r^{\,l}+\beta_{l,m}\,r^{-(l+1)}\right]Y_{l,m}(\theta,\varphi).$

(327)

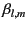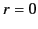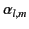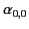If the domain of solution includes the origin then all of the $\beta_{l,m}$ must be zero, in order to ensure that the potential remains finite at . On the other hand, if the domain of solution extends to infinity then all of the $\alpha_{l,m}$ (except $\alpha_{0,0}$ ) must be zero, otherwise the potential would be infinite at $r=\infty$ .

Next: Poisson's Equation in Spherical Up: Potential Theory Previous: Spherical Harmonics

Richard Fitzpatrick 2014-06-27