


Next: Dirichlet Green's Function for
Up: Electrostatic Fields
Previous: Green's Theorem
Boundary Value Problems
Consider a volume  bounded by a surface
bounded by a surface  . Suppose that we wish to solve Poisson's equation,
. Suppose that we wish to solve Poisson's equation,
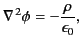 |
(238) |
throughout  , subject to given Dirichlet or Neumann boundary conditions on
, subject to given Dirichlet or Neumann boundary conditions on  . The charge density distribution,
. The charge density distribution,
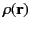 ,
is assumed to be known throughout
,
is assumed to be known throughout  . This type of problem is called a boundary value problem.
. This type of problem is called a boundary value problem.
Similarly to the approach taken in Section 2.3, we can solve Poisson's equation by means of a Green's function,
 ,
that satisfies
,
that satisfies
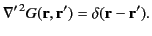 |
(239) |
In fact, it follows from Equation (25) [because
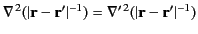 , by symmetry] that
, by symmetry] that
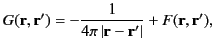 |
(240) |
where
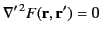 |
(241) |
throughout  . Here, the function
. Here, the function
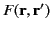 is chosen in such a manner as to satisfy the boundary
conditions on
is chosen in such a manner as to satisfy the boundary
conditions on  . Making use of Green's theorem, (220), where
. Making use of Green's theorem, (220), where
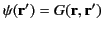 ,
we find that
,
we find that
![$\displaystyle \phi({\bf r})=-\frac{1}{\epsilon_0} \int_V G({\bf r},{\bf r}')\,\...
...'}-\phi({\bf r}')\,\frac{\partial G({\bf r},{\bf r}')}{\partial n'}\right]d S'.$](img547.png) |
(242) |
Here, use has been made of Equations (23), (238), and (239).
Note, incidentally, that the divergence theorem, combined with Equation (239), yields
 |
(243) |
Consider the Dirichlet problem in which
 is known on
is known on  , but
, but
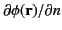 is unknown. We
can construct an appropriate Green's function for this problem,
is unknown. We
can construct an appropriate Green's function for this problem,
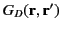 ,
where
,
where
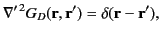 |
(244) |
by choosing the function
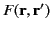 in Equation (240) in such a manner that
in Equation (240) in such a manner that
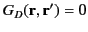 |
(245) |
when  lies on
lies on  . It then follows from
Equation (242) that
. It then follows from
Equation (242) that
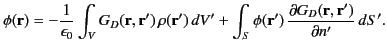 |
(246) |
Hence, the potential
 is specified in terms of integrals over known functions throughout
is specified in terms of integrals over known functions throughout  and on
and on  .
.
It is possible to prove that the Dirichlet Green's function is symmetric with respect to its arguments. In other
words,
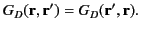 |
(247) |
Making use of Green's theorem, (220), where
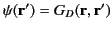 and
and
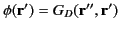 ,
we find that
,
we find that
However, by definition,
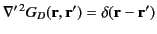 ,
,
 ,
and
,
and
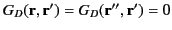 when
when  lies on
lies on  .
Hence,
.
Hence,
![$\displaystyle \int_V\left[G_D({\bf r},{\bf r}')\,\delta({\bf r}''-{\bf r}')-G_D({\bf r}'',{\bf r}')\,\delta({\bf r}-{\bf r}')\right]dV'=0,$](img561.png) |
(248) |
which yields
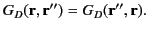 |
(249) |
It is also possible to demonstrate that the Dirichlet Green's function is unique. Proceeding in the usual fashion, suppose that there
are two different functions,
 and
and
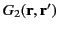 , that both satisfy Equations (244) and (245).
It follows that
, that both satisfy Equations (244) and (245).
It follows that
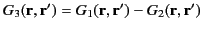 satisfies
satisfies
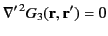 |
(250) |
throughout  , subject to the boundary
condition
, subject to the boundary
condition
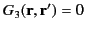 |
(251) |
when  lies on
lies on  . However, we saw in Section 2.2 that the only solution to this problem is
. However, we saw in Section 2.2 that the only solution to this problem is
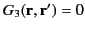 for
for  in
in  or on
or on  . Hence, the functions
. Hence, the functions
 and
and
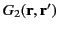 are identical, and the
Dirichlet Green's function is unique. It follows that the potential specified in Equation (246) is also unique.
are identical, and the
Dirichlet Green's function is unique. It follows that the potential specified in Equation (246) is also unique.
Consider the Neumann problem in which
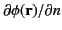 is known on
is known on  , but
, but
 is unknown.
In this case, the obvious ansatz,
is unknown.
In this case, the obvious ansatz,
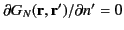 when
when  lies on
lies on  , is incorrect, because it is inconsistent
with the constraint (243). The simplest ansatz that works is a choice of
, is incorrect, because it is inconsistent
with the constraint (243). The simplest ansatz that works is a choice of
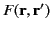 in Equation (240) such that
in Equation (240) such that
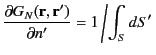 |
(252) |
when  lies on
lies on  . Hence, Equation (242) yields
. Hence, Equation (242) yields
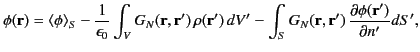 |
(253) |
where
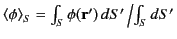 is the average value of the potential on
is the average value of the potential on  . This average value can
be absorbed into the arbitrary constant that can always be added to a scalar potential. Thus, the potential is again specified in terms of integrals over known functions throughout
. This average value can
be absorbed into the arbitrary constant that can always be added to a scalar potential. Thus, the potential is again specified in terms of integrals over known functions throughout  and on
and on  .
.
It is possible to prove that the Neumann Green's function can be chosen in such a manner that it is symmetric with respect to its arguments. In other
words,
 |
(254) |
Consider a Neumann Green's function that is not symmetric with respect to its arguments. That is, an asymmetric function
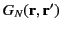 which satisfies
which satisfies
 |
(255) |
and
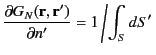 |
(256) |
when  lies on
lies on  . Consider
. Consider
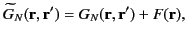 |
(257) |
where
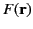 is arbitrary.
It follows that
is arbitrary.
It follows that
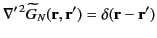 |
(258) |
and
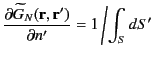 |
(259) |
when  lies on
lies on  . Hence,
. Hence,
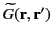 is also a valid Neumann Green's function. Making use of Green's theorem, (220), where
is also a valid Neumann Green's function. Making use of Green's theorem, (220), where
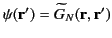 and
and
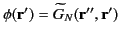 ,
we find that
,
we find that
![$\displaystyle \widetilde{G}_N({\bf r},{\bf r}'')-\widetilde{G}_N({\bf r}'',{\bf...
...{\bf r}')-\widetilde{G}_N({\bf r}'',{\bf r}')\right]dS'\left/\int_S dS'\right..$](img580.png) |
(260) |
We deduce that
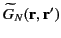 is symmetric provided that
is symmetric provided that
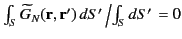 . We
can ensure that this is the case by choosing
. We
can ensure that this is the case by choosing
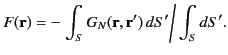 |
(261) |
Thus, given an asymmetric Neumann Green's function, it is always possible to construct a symmetric Green's function that satisfies
and
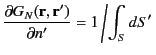 |
(264) |
when  lies on
lies on  .
.
We can also show that the symmetric Neumann Green's function is unique. Proceeding in the usual fashion, suppose that there
are two different functions,
 and
and
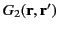 , that both satisfy Equations (263)--(265).
It follows that
, that both satisfy Equations (263)--(265).
It follows that
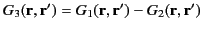 satisfies
satisfies
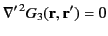 |
(265) |
throughout  , subject to the boundary
condition
, subject to the boundary
condition
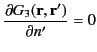 |
(266) |
when  lies on
lies on  . Equation (130) can be written
. Equation (130) can be written
![$\displaystyle \int_S \phi({\bf r}')\,\frac{\partial\phi}{\partial n'}\,dS' = \int_V\left[\phi({\bf r}')\,\nabla'^{\,2}\phi+\nabla'\phi\cdot\nabla'\phi\right]dV'.$](img588.png) |
(267) |
Suppose that
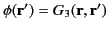 . It follows that
. It follows that
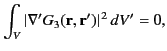 |
(268) |
which implies that
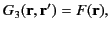 |
(269) |
where
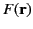 is arbitrary.
However,
is arbitrary.
However,
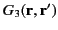 also
satisfies
also
satisfies
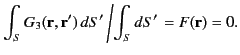 |
(270) |
Hence,
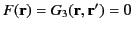 , and the Green's function is unique. It follows that the potential specified in Equation (254) is also unique (up to an
arbitrary additive constant).
, and the Green's function is unique. It follows that the potential specified in Equation (254) is also unique (up to an
arbitrary additive constant).
Finally, the fact that the Green's function for Poisson's equation,
 , is (or can be chosen to be) symmetric implies from Equation (239) that
, is (or can be chosen to be) symmetric implies from Equation (239) that
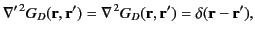 |
(271) |
because
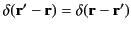 .
.



Next: Dirichlet Green's Function for
Up: Electrostatic Fields
Previous: Green's Theorem
Richard Fitzpatrick
2014-06-27
![]() ,
that satisfies
,
that satisfies
![]() is known on
is known on ![]() , but
, but
![]() is unknown. We
can construct an appropriate Green's function for this problem,
is unknown. We
can construct an appropriate Green's function for this problem,
![]() ,
where
,
where
![\begin{multline}
\int_V\left[G_D({\bf r},{\bf r}')\,\nabla'^{\,2}G_D({\bf r}'',{...
...')\,\frac{\partial G_D({\bf r},{\bf r}')}{\partial n'}\right]dS'.
\end{multline}](img557.png)
![$\displaystyle \int_V\left[G_D({\bf r},{\bf r}')\,\delta({\bf r}''-{\bf r}')-G_D({\bf r}'',{\bf r}')\,\delta({\bf r}-{\bf r}')\right]dV'=0,$](img561.png)
![]() and
and
![]() , that both satisfy Equations (244) and (245).
It follows that
, that both satisfy Equations (244) and (245).
It follows that
![]() satisfies
satisfies
![]() is known on
is known on ![]() , but
, but
![]() is unknown.
In this case, the obvious ansatz,
is unknown.
In this case, the obvious ansatz,
![]() when
when ![]() lies on
lies on ![]() , is incorrect, because it is inconsistent
with the constraint (243). The simplest ansatz that works is a choice of
, is incorrect, because it is inconsistent
with the constraint (243). The simplest ansatz that works is a choice of
![]() in Equation (240) such that
in Equation (240) such that
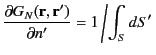
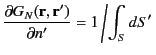
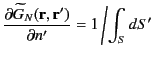
![$\displaystyle \widetilde{G}_N({\bf r},{\bf r}'')-\widetilde{G}_N({\bf r}'',{\bf...
...{\bf r}')-\widetilde{G}_N({\bf r}'',{\bf r}')\right]dS'\left/\int_S dS'\right..$](img580.png)
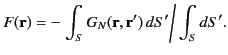
![]() and
and
![]() , that both satisfy Equations (263)--(265).
It follows that
, that both satisfy Equations (263)--(265).
It follows that
![]() satisfies
satisfies
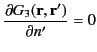
![$\displaystyle \int_S \phi({\bf r}')\,\frac{\partial\phi}{\partial n'}\,dS' = \int_V\left[\phi({\bf r}')\,\nabla'^{\,2}\phi+\nabla'\phi\cdot\nabla'\phi\right]dV'.$](img588.png)
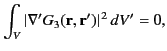
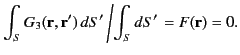
![]() , is (or can be chosen to be) symmetric implies from Equation (239) that
, is (or can be chosen to be) symmetric implies from Equation (239) that