- ... is
![[*]](footnote.png)
- In principle,
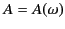 and
and
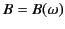 , with
, with 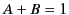 . However, we shall
demonstrate, later on, that
. However, we shall
demonstrate, later on, that 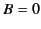 , otherwise causality is violated. It follows
that
, otherwise causality is violated. It follows
that 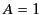 . Thus, it is legitimate to assume, for the moment, that
. Thus, it is legitimate to assume, for the moment, that
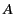 and
and 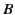 are independent of
are independent of 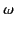 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
kind.
![[*]](footnote.png)
-
J.D. Jackson,
Classical Electrodynamics, 2nd Edition, (Wiley, 1962), p. 104.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... that
![[*]](footnote.png)
- A. Sommerfeld,
Partial Differential Equations in Physics, (Academic Press,
New York, 1964), p. 117.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form
![[*]](footnote.png)
- J.D. Jackson,
Classical Electrodynamics, 2nd Edition, (Wiley, 1962). Section 3.5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... that
![[*]](footnote.png)
- Ibid. Section 3.2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form
![[*]](footnote.png)
- Ibid. Section 3.5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... that
![[*]](footnote.png)
- Ibid. Section 3.6.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
is
![[*]](footnote.png)
- M. Abramowitz, and I. Stegun (eds.), Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables,
(Dover, New York, 1965). Chapter 9.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... books.
![[*]](footnote.png)
- Ibid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
is
![[*]](footnote.png)
- Ibid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... where
![[*]](footnote.png)
- Ibid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... identity
![[*]](footnote.png)
- Ibid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integrals,
![[*]](footnote.png)
- J.D. Jackson,
Classical Electrodynamics, 2nd Edition, (Wiley, 1962). Section 5.5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... even.
![[*]](footnote.png)
- Ibid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... that
![[*]](footnote.png)
- Ibid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... known,
![[*]](footnote.png)
- M. Abramowitz,
and I.A. Stegun, Handbook of Mathematical Functions, (Dover, New York,
1965). Equation 9.1.21.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integrals,
![[*]](footnote.png)
- M. Abramowitz,
and I.A. Stegun, Handbook of Mathematical Functions, (Dover, New York,
1965). Section 7.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... decent.
![[*]](footnote.png)
- Léon Brillouin,
Wave Propagation and Group Velocity,
(Academic Press, New York, 1960).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
decent
![[*]](footnote.png)
- Ibid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1857.
![[*]](footnote.png)
- G.G. Stokes, Trans. Camb. Phil. Soc. 10, 106-128
(1857).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... convention.
![[*]](footnote.png)
- Here, we are assuming that
the laws of physics do not possess an intrinsic handedness. This is certainly
the case for mechanics and electromagnetism. However, the weak interaction
does possess an intrinsic handedness: that is, it is fundamentally
different in a parity inverted universe. So, the equations governing the
weak interaction do actually contain mixtures of tensors and pseudo-tensors.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)
![[*]](footnote.png)