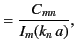Next: Poisson's Equation in Cylindrical
Up: Potential Theory
Previous: Newmann Problem in Spherical
Laplace's Equation in Cylindrical Coordinates
Suppose that we wish to solve Laplace's equation,
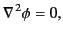 |
(392) |
within a cylindrical volume of radius 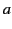 and height
and height 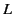 . Let us adopt the standard cylindrical coordinates,
. Let us adopt the standard cylindrical coordinates, 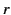 ,
,  ,
,  . Suppose that the curved portion of the bounding surface
corresponds to
. Suppose that the curved portion of the bounding surface
corresponds to  , while the two flat portions correspond to
, while the two flat portions correspond to 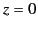 and
and 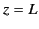 , respectively.
Suppose, finally, that the boundary conditions that are imposed at the bounding surface are
, respectively.
Suppose, finally, that the boundary conditions that are imposed at the bounding surface are
where
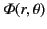 is a given function. In other words, the potential is zero on the curved and bottom surfaces of the cylinder, and specified
on the top surface.
is a given function. In other words, the potential is zero on the curved and bottom surfaces of the cylinder, and specified
on the top surface.
In cylindrical coordinates, Laplace's equation is written
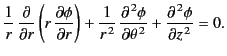 |
(396) |
Let us try a separable solution of the form
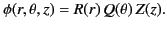 |
(397) |
Proceeding in the usual manner, we obtain
Note that we have selected exponential, rather than oscillating, solutions in the  -direction [by writing
-direction [by writing
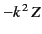 , instead of
, instead of
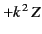 , in Equation (399)]. As
will become clear, this implies that the radial solutions oscillate, which is the appropriate choice for the particular set of boundary conditions under consideration.
The solution to Equation (399), subject to the constraint that
, in Equation (399)]. As
will become clear, this implies that the radial solutions oscillate, which is the appropriate choice for the particular set of boundary conditions under consideration.
The solution to Equation (399), subject to the constraint that  [which follows from the first boundary condition, (394)] is
[which follows from the first boundary condition, (394)] is
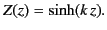 |
(401) |
The most general solution to Equation (400) is
![$\displaystyle Q(\theta) = \sum_{m=0,\infty}\left[A_m\,\cos (m\,\theta) + B_m\,\sin(m\,\theta)\right].$](img879.png) |
(402) |
Note that, to ensure that the potential is single-valued in  , the constant
, the constant  is constrained to be an integer.
Finally, if we write
is constrained to be an integer.
Finally, if we write 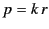 then Equation (401) becomes
then Equation (401) becomes
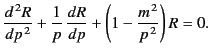 |
(403) |
This equation is known as Bessel's equation. The standard solution of this equation that is well behaved at 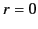 is
is![[*]](footnote.png)
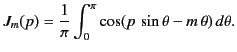 |
(404) |
This solution, which is known as a Bessel function, has the properties that
In other words, at small arguments the function has a power-law behavior, whereas at large arguments it takes the form
of an oscillation of slowly decaying amplitude.
It follows that
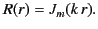 |
(407) |
Let 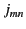 denote the
denote the  th zero of the Bessel function
th zero of the Bessel function 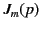 . In other words,
. In other words, 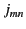 is the
is the  th root (in order, as
th root (in order, as  increases
from zero) of
increases
from zero) of 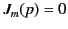 . The values of the
. The values of the 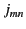 can be looked up in standard reference books.
can be looked up in standard reference books.![[*]](footnote.png) (For example,
(For example,
 and
and
 .) We can satisfy our second boundary condition, (395), by making the choice
.) We can satisfy our second boundary condition, (395), by making the choice  ,
where
,
where
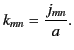 |
(408) |
Thus, our separable solution becomes
![$\displaystyle \phi(r,\theta,z) = \sum_{m=0,\infty}\sum_{n=1,\infty} \sinh(j_{mn...
...\,J_m(j_{mn}\,r/a)\left[A_{mn}\,\cos(m\,\theta)+B_{mn}\,\sin(m\,\theta)\right].$](img897.png) |
(409) |
It is convenient to express the specified function
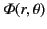 in the form of a Fourier series: that is,
in the form of a Fourier series: that is,
![$\displaystyle {\mit\Phi}(r,\theta) =\sum_{m=0,\infty}\left[C_m(r)\,\cos(m\,\theta)+S_m(r)\,\sin(m\,\theta)\right].$](img898.png) |
(410) |
Our final boundary condition, (396), then yields
It remains to invert the previous two expressions to obtain the coefficients 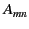 and
and 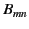 . In fact,
it is possible to demonstrate that if
. In fact,
it is possible to demonstrate that if
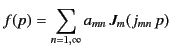 |
(413) |
then
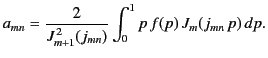 |
(414) |
Hence,
and our solution is fully determined.
Consider the limit that
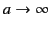 . In this case, according to Equation (409), the allowed values of
. In this case, according to Equation (409), the allowed values of 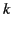 become more and
more closely spaced. Consequently, the sum over discrete
become more and
more closely spaced. Consequently, the sum over discrete 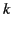 -values in (410) morphs into an integral over a continuous range of
-values in (410) morphs into an integral over a continuous range of 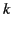 -values.
For instance, suppose that we wish to solve Laplace's equation in the region
-values.
For instance, suppose that we wish to solve Laplace's equation in the region 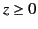 , subject to the boundary condition that
, subject to the boundary condition that
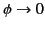 as
as
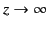 and
and
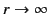 , with
, with
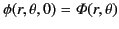 , where
, where
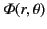 is specified. In this case, we would choose
is specified. In this case, we would choose
 in order to satisfy the boundary condition at large
in order to satisfy the boundary condition at large  . The
choice
. The
choice
 ensures that the potential is well behaved at
ensures that the potential is well behaved at 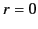 , and automatically satisfies the boundary condition at large
, and automatically satisfies the boundary condition at large 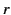 .
Hence, our general solution becomes
.
Hence, our general solution becomes
![$\displaystyle \phi(r,\theta,z) = \sum_{m=0,\infty} \int_0^\infty {\rm e}^{-k\,z}\,J_m(k\,r)\,\left[A_m(k)\,\cos (m\,\theta)+B_m(k)\,\sin(m\,\theta)\right]\,dk.$](img919.png) |
(417) |
If we write
![$\displaystyle {\mit\Phi}(r,\theta) = \sum_{m=0,\infty}\left[C_m(r)\,\cos(m\,\theta)+ S_m(r)\,\sin(m\,\theta)\right]$](img920.png) |
(418) |
then the final boundary condition implies that
We can invert the previous two expressions by means of the identity
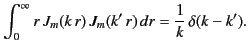 |
(421) |
Hence, we obtain
and our solution is fully defined.
Suppose that we wish to solve Laplace's equation in a cylindrical volume of radius 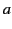 and height
and height 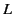 , subject to the
boundary conditions
, subject to the
boundary conditions
where
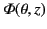 is specified. In other words, the potential is zero on the two flat portions of the bounding surface, and
given on the curved portion. We can again look for a separable solution of the form (398).
Proceeding in the usual manner, we obtain
is specified. In other words, the potential is zero on the two flat portions of the bounding surface, and
given on the curved portion. We can again look for a separable solution of the form (398).
Proceeding in the usual manner, we obtain
Note that we have selected oscillating, rather than exponential solutions in the  -direction [by writing
-direction [by writing
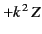 , instead of
, instead of
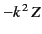 , in Equation (428)]. This is the appropriate choice for the particular set of boundary conditions under
consideration. The solution to Equation (428), subject to the constraints that
, in Equation (428)]. This is the appropriate choice for the particular set of boundary conditions under
consideration. The solution to Equation (428), subject to the constraints that
 [which follow from
the boundary conditions (425) and (426)] is
[which follow from
the boundary conditions (425) and (426)] is
 |
(430) |
where
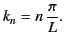 |
(431) |
Here,  is a positive integer. The single-valued solution to Equation (429) is again
is a positive integer. The single-valued solution to Equation (429) is again
![$\displaystyle Q(\theta) = \sum_{m=0,\infty}\left[A_m\,\cos (m\,\theta) + B_m\,\sin(m\,\theta)\right].$](img879.png) |
(432) |
Finally, writing 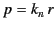 , Equation (430) takes the form
, Equation (430) takes the form
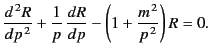 |
(433) |
This equation is known as the modified Bessel equation. The standard solution of this equation that is well behaved at 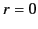 is
is![[*]](footnote.png)
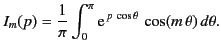 |
(434) |
This solution, which is known as a modified Bessel function, has the properties that
In other words, at small arguments the function has a power-law behavior, whereas at large arguments it grows exponentially. It
follows that
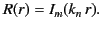 |
(437) |
Thus, our separable solution becomes
![$\displaystyle \phi(r,\theta,z) =\sum_{m=0,\infty} \sum_{n=1,\infty}\sin(k_n\,z)\,I_m(k_n\,z)\left[A_{mn}\,\cos(m\,\theta)+B_{mn}\,\sin(m\,\theta)\right].$](img943.png) |
(438) |
If we express the function
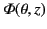 as a Fourier series in
as a Fourier series in  and
and  , so that
, so that
![$\displaystyle {\mit\Phi}(\theta,z) = \sum_{m=0,\infty}\sum_{n=1,\infty}\sin(k_n\,z)\left[C_{mn}\,\cos(m\,\theta)+S_{mn}\,\sin(m\,\theta)\right],$](img944.png) |
(439) |
then the boundary condition (427) yields
Hence, our solution is fully specified.



Next: Poisson's Equation in Cylindrical
Up: Potential Theory
Previous: Newmann Problem in Spherical
Richard Fitzpatrick
2014-06-27
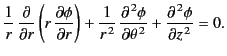
![$\displaystyle Q(\theta) = \sum_{m=0,\infty}\left[A_m\,\cos (m\,\theta) + B_m\,\sin(m\,\theta)\right].$](img879.png)
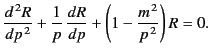
![[*]](footnote.png)
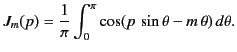

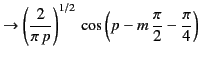
![[*]](footnote.png) (For example,
(For example,
![$\displaystyle {\mit\Phi}(r,\theta) =\sum_{m=0,\infty}\left[C_m(r)\,\cos(m\,\theta)+S_m(r)\,\sin(m\,\theta)\right].$](img898.png)
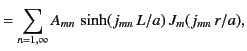

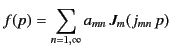
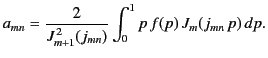
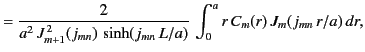
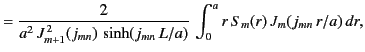
![]() . In this case, according to Equation (409), the allowed values of
. In this case, according to Equation (409), the allowed values of ![]() become more and
more closely spaced. Consequently, the sum over discrete
become more and
more closely spaced. Consequently, the sum over discrete ![]() -values in (410) morphs into an integral over a continuous range of
-values in (410) morphs into an integral over a continuous range of ![]() -values.
For instance, suppose that we wish to solve Laplace's equation in the region
-values.
For instance, suppose that we wish to solve Laplace's equation in the region ![]() , subject to the boundary condition that
, subject to the boundary condition that
![]() as
as
![]() and
and
![]() , with
, with
![]() , where
, where
![]() is specified. In this case, we would choose
is specified. In this case, we would choose
![]() in order to satisfy the boundary condition at large
in order to satisfy the boundary condition at large ![]() . The
choice
. The
choice
![]() ensures that the potential is well behaved at
ensures that the potential is well behaved at ![]() , and automatically satisfies the boundary condition at large
, and automatically satisfies the boundary condition at large ![]() .
Hence, our general solution becomes
.
Hence, our general solution becomes
![$\displaystyle \phi(r,\theta,z) = \sum_{m=0,\infty} \int_0^\infty {\rm e}^{-k\,z}\,J_m(k\,r)\,\left[A_m(k)\,\cos (m\,\theta)+B_m(k)\,\sin(m\,\theta)\right]\,dk.$](img919.png)
![$\displaystyle {\mit\Phi}(r,\theta) = \sum_{m=0,\infty}\left[C_m(r)\,\cos(m\,\theta)+ S_m(r)\,\sin(m\,\theta)\right]$](img920.png)
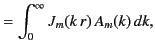
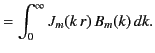
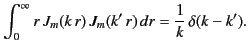
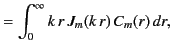

![]() and height
and height ![]() , subject to the
boundary conditions
, subject to the
boundary conditions
![$\displaystyle Q(\theta) = \sum_{m=0,\infty}\left[A_m\,\cos (m\,\theta) + B_m\,\sin(m\,\theta)\right].$](img879.png)
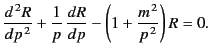
![[*]](footnote.png)


![$\displaystyle \phi(r,\theta,z) =\sum_{m=0,\infty} \sum_{n=1,\infty}\sin(k_n\,z)\,I_m(k_n\,z)\left[A_{mn}\,\cos(m\,\theta)+B_{mn}\,\sin(m\,\theta)\right].$](img943.png)
![$\displaystyle {\mit\Phi}(\theta,z) = \sum_{m=0,\infty}\sum_{n=1,\infty}\sin(k_n\,z)\left[C_{mn}\,\cos(m\,\theta)+S_{mn}\,\sin(m\,\theta)\right],$](img944.png)