Next: Retarded Potentials
Up: Maxwell's Equations
Previous: Three-Dimensional Dirac Delta Function
Equation (14), as well as the three Cartesian components of Equation (15), are
inhomogeneous three-dimensional wave equations of the general form
 |
(30) |
where
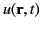 is an unknown potential, and
is an unknown potential, and
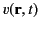 a known source function.
Let us investigate whether it is possible to find a unique solution of this type of equation.
a known source function.
Let us investigate whether it is possible to find a unique solution of this type of equation.
Let us assume
that the source function
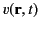 can be expressed as a
Fourier integral,
can be expressed as a
Fourier integral,
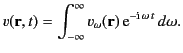 |
(31) |
The inverse transform is
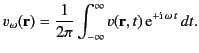 |
(32) |
Similarly, we can write the general potential
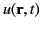 as a
Fourier integral,
as a
Fourier integral,
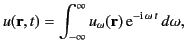 |
(33) |
with the corresponding inverse
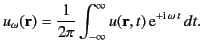 |
(34) |
Fourier transformation of Equation (30) yields
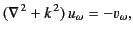 |
(35) |
where
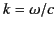 .
.
Equation (35), which reduces to Poisson's equation (see Section 2.3),
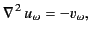 |
(36) |
in the limit
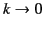 , is known as Helmholtz's equation. Because Helmholtz's equation is linear,
it is appropriate to attempt a Green's function method of solution. Let us
try to find a Green's function,
, is known as Helmholtz's equation. Because Helmholtz's equation is linear,
it is appropriate to attempt a Green's function method of solution. Let us
try to find a Green's function,
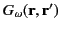 , such that
, such that
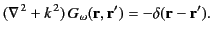 |
(37) |
The general solution to Equation (35) is then [cf., Equation (142)]
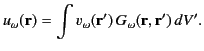 |
(38) |
Let us adopt the spatial boundary condition
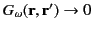 as
as
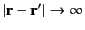 , so as to ensure that the potential goes to zero a long way from the source.
Because Equation (37) is spherically symmetric about the
point
, so as to ensure that the potential goes to zero a long way from the source.
Because Equation (37) is spherically symmetric about the
point  , it is plausible that the
Green's function itself is spherically symmetric: that is,
, it is plausible that the
Green's function itself is spherically symmetric: that is,
 . In this case, Equation (37) reduces to
. In this case, Equation (37) reduces to
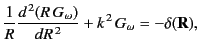 |
(39) |
where
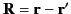 , and
, and
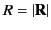 . The most general solution
to the above equation in the region
. The most general solution
to the above equation in the region  is
is![[*]](footnote.png)
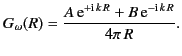 |
(40) |
However, we know that
Helmholtz's equation tends towards Poisson's equation in the limit
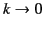 . It stands to reason that the
Green's function for Helmholtz's equation much tend toward that for Poisson's equation in the same limit.
Now, the Green's function for Poisson's equation, (36), satisfies
. It stands to reason that the
Green's function for Helmholtz's equation much tend toward that for Poisson's equation in the same limit.
Now, the Green's function for Poisson's equation, (36), satisfies
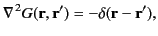 |
(41) |
as well as the usual constraint that
 as
as
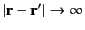 . It follows from Equation (25) that
. It follows from Equation (25) that
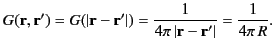 |
(42) |
Thus, the condition that
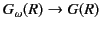 as
as
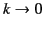 implies that
implies that 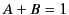 .
.
Reconstructing
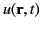 from Equations (33), (38), and
(40), we obtain
from Equations (33), (38), and
(40), we obtain
![$\displaystyle u({\bf r}, t) = \frac{1}{4\pi} \int\! \int\frac{ v_\omega({\bf r'...
...mega\,(t-R/c)}+ B \,{\rm e}^{-{\rm i}\, \omega\,(t+R/c)} \right]\,d\omega\,dV'.$](img140.png) |
(43) |
It follows from Equation (31) that
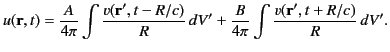 |
(44) |
Now, the real-space Green's function for the
inhomogeneous three-dimensional wave equation, (30), satisfies
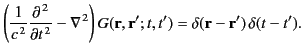 |
(45) |
Hence, the most general solution of Equation (30) takes the form
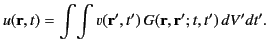 |
(46) |
Comparing Equations (44) and (46), we obtain
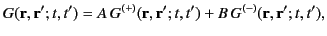 |
(47) |
where
![$\displaystyle G^{(\pm)} ({\bf r}, {\bf r}'; t, t') = \frac{\delta(t'-[t\mp \vert{\bf r}- {\bf r'}\vert/c])}{4\pi \,\vert{\bf r}-{\bf r}'\vert},$](img145.png) |
(48) |
and 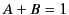 .
.
The real-space Green's function specifies the response of the system
to a point source located at position  that
appears momentarily at time
that
appears momentarily at time 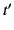 . According to the retarded Green's
function,
. According to the retarded Green's
function, 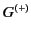 , this response consists of a spherical wave, centered
on the point
, this response consists of a spherical wave, centered
on the point  , that propagates forward in time.
In order for the wave to reach position
, that propagates forward in time.
In order for the wave to reach position  at time
at time 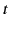 , it must
have been emitted from the source at
, it must
have been emitted from the source at 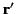 at the retarded
time
at the retarded
time
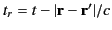 . According to the
advanced Green's function,
. According to the
advanced Green's function, 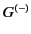 , the response consists of a
spherical wave, centered
on the point
, the response consists of a
spherical wave, centered
on the point  , that propagates backward in time. Clearly, the advanced
potential is not consistent with our ideas about causality, which
demand that an effect can never precede its cause in time. Thus, the
Green's function that is consistent with our experience is
, that propagates backward in time. Clearly, the advanced
potential is not consistent with our ideas about causality, which
demand that an effect can never precede its cause in time. Thus, the
Green's function that is consistent with our experience is
![$\displaystyle G ({\bf r}, {\bf r}'; t, t')= G^{(+)} ({\bf r}, {\bf r}'; t, t') ...
...ta(t'-[t - \vert{\bf r}- {\bf r'}\vert/c])}{4\pi \,\vert{\bf r}-{\bf r}'\vert}.$](img152.png) |
(49) |
Incidentally, we are able to find solutions of the inhomogeneous wave equation,
(30), that
propagate backward in time because this equation is time symmetric
(i.e., it is invariant under the transformation
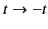 ).
).
In conclusion, the most general solution of the inhomogeneous wave equation,
(30), that satisfies sensible boundary conditions at infinity, and
is consistent with causality, is
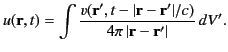 |
(50) |
This expression is sometimes written
![$\displaystyle u({\bf r}, t) = \int \frac{ [v({\bf r}')]} {4\pi\,\vert{\bf r} - {\bf r}'\vert}\,dV',$](img155.png) |
(51) |
where the rectangular bracket symbol ![$ [\,]$](img156.png) denotes that the terms inside the
bracket are to be evaluated at the retarded time
denotes that the terms inside the
bracket are to be evaluated at the retarded time
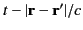 .
Note, in particular, from Equation (50), that if there is no source
[i.e., if
.
Note, in particular, from Equation (50), that if there is no source
[i.e., if
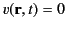 ] then there is no field
[i.e.,
] then there is no field
[i.e.,
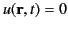 ]. But, is expression (50) really the only solution of Equation (30) that
satisfies sensible boundary conditions at infinity? In other words, is this solution really unique?
Unfortunately, there is a weak link in our derivation--between Equations (38) and (39)--where we assumed, without proof, that the Green's function for Helmholtz's equation, subject to the boundary condition
]. But, is expression (50) really the only solution of Equation (30) that
satisfies sensible boundary conditions at infinity? In other words, is this solution really unique?
Unfortunately, there is a weak link in our derivation--between Equations (38) and (39)--where we assumed, without proof, that the Green's function for Helmholtz's equation, subject to the boundary condition
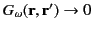 as
as
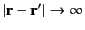 , is spherically symmetric. Let us try
to fix this problem.
, is spherically symmetric. Let us try
to fix this problem.
With the benefit of hindsight, we can see that the Fourier-space Green's function
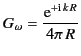 |
(52) |
corresponds to the retarded solution in real space, and is, therefore, the
correct physical Green's function in Fourier space. The Fourier-space Green's function
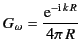 |
(53) |
corresponds to the advanced solution in real space, and must, therefore,
be rejected.
We can select the retarded Green's function in Fourier space by imposing the following
boundary condition at infinity
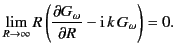 |
(54) |
This is called the Sommerfeld radiation condition, and basically
ensures that infinity is an absorber of radiation, but not a source.
But, does this boundary condition uniquely select the spherically
symmetric Green's function (52) as the solution of
 |
(55) |
Here,
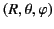 are spherical polar coordinates. If it does
then we can be sure that Equation (50) represents the unique solution of
the inhomogeneous wave equation, (30), that is consistent with causality.
are spherical polar coordinates. If it does
then we can be sure that Equation (50) represents the unique solution of
the inhomogeneous wave equation, (30), that is consistent with causality.
Let us suppose that there are two different solutions of Equation (55), both of which satisfy
the boundary condition (54), and revert to the unique (see Section 2.3)
Green's function
for Poisson's equation, (42), in the limit
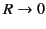 . Let us
call these solutions
. Let us
call these solutions  and
and 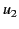 , and let us form the difference
, and let us form the difference
 . Consider a surface
. Consider a surface 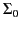 which is a sphere of arbitrarily
small radius centred on the origin. Consider a second surface
which is a sphere of arbitrarily
small radius centred on the origin. Consider a second surface
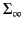 which is a sphere of arbitrarily large radius centred on the
origin. Let
which is a sphere of arbitrarily large radius centred on the
origin. Let  denote the volume enclosed by these surfaces.
The difference function
denote the volume enclosed by these surfaces.
The difference function  satisfies the homogeneous Helmholtz equation,
satisfies the homogeneous Helmholtz equation,
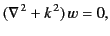 |
(56) |
throughout  .
According to the generalized (to deal with complex potentials) Green's theorem (see Section 2.9),
.
According to the generalized (to deal with complex potentials) Green's theorem (see Section 2.9),
 |
(57) |
where
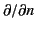 denotes a derivative normal to the surface in
question. It is clear from Equation (56) that the volume integral is
zero. It is also clear that the first surface integral is zero, because
both
denotes a derivative normal to the surface in
question. It is clear from Equation (56) that the volume integral is
zero. It is also clear that the first surface integral is zero, because
both  and
and 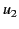 must revert to the Green's function for
Poisson's equation in the limit
must revert to the Green's function for
Poisson's equation in the limit
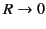 . Thus,
. Thus,
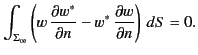 |
(58) |
Equation (56) can be written
 |
(59) |
where 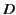 is the spherical harmonic operator
is the spherical harmonic operator
 |
(60) |
The most general solution to Equation (59) takes the form
![$\displaystyle w(R,\theta,\varphi) =\sum_{l,m=0,\infty} \left[ C_{l,m}\, h_l^{(1)}(k\,R) + D_{l,m}\, h_l^{(2)}(k\,R) \right] Y_{l,m}(\theta,\varphi).$](img179.png) |
(61) |
Here, the 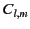 and
and 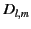 are arbitrary coefficients, the
are arbitrary coefficients, the
 are spherical harmonics (see Section 3.3), and
are spherical harmonics (see Section 3.3), and
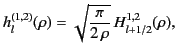 |
(62) |
where the 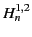 are Hankel functions of the first and second
kind.
are Hankel functions of the first and second
kind.![[*]](footnote.png) It can be demonstrated that
It can be demonstrated that![[*]](footnote.png)
where
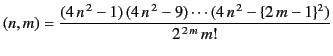 |
(65) |
and 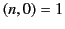 . Note that the summations in Equations (63) and (64) terminate after
. Note that the summations in Equations (63) and (64) terminate after
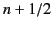 terms.
terms.
The large-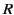 behavior of the
behavior of the
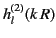 functions is clearly inconsistent
with the Sommerfeld radiation condition, (54). It follows that
all of the
functions is clearly inconsistent
with the Sommerfeld radiation condition, (54). It follows that
all of the 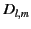 in Equations (61) are zero. The most general solution can
now be expressed in the form
in Equations (61) are zero. The most general solution can
now be expressed in the form
 |
(66) |
where the
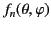 are various weighted sums of the spherical harmonics.
Substitution of this solution into the differential equation (59)
yields
are various weighted sums of the spherical harmonics.
Substitution of this solution into the differential equation (59)
yields
![$\displaystyle {\rm e}^{+{\rm i}\,k\,R} \sum_{n=0,\infty} \left[-\frac{2\,{\rm i...
...n}{R^{\,n+1}} +\frac{n\,(n+1)}{R^{\,n+2}} + \frac{D}{R^{\,n+2}}\right] f_n = 0.$](img195.png) |
(67) |
Replacing the index of summation  in the first term of the parentheses
by
in the first term of the parentheses
by 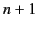 , we obtain
, we obtain
![$\displaystyle {\rm e}^{+{\rm i}\,k\,R} \sum_{n=0\,\infty} \frac{-2\,{\rm i}\,k\, (n+1) \,f_{n+1} + [n\,(n+1)+D]\,f_n }{R^{\,n+2}} =0,$](img198.png) |
(68) |
which yields the recursion relation
![$\displaystyle 2\,{\rm i} \,k\,(n+1) f_{n+1} = [n\,(n+1)+D]\,f_n.$](img199.png) |
(69) |
It follows that if 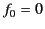 then all of the
then all of the 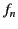 are equal to zero.
are equal to zero.
Let us now consider the surface integral (58). Because we are interested in
the limit
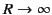 , we can replace
, we can replace  by the first term of
its expansion in (66), so that
by the first term of
its expansion in (66), so that
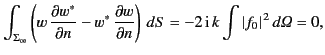 |
(70) |
where
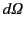 is an element of solid angle. It is clear that
is an element of solid angle. It is clear that 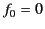 .
This implies that
.
This implies that
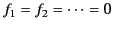 , and, hence, that
, and, hence, that 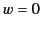 . Thus,
there is only one solution of Equation (55) that is consistent with
the Sommerfeld radiation condition, and this is given by Equation (52).
We can now be sure that Equation (50) is the unique solution of
Equation (30), subject to the boundary condition (54). This boundary
condition ensures that infinity is an absorber of electromagnetic radiation, but
not an emitter, which seems entirely reasonable.
. Thus,
there is only one solution of Equation (55) that is consistent with
the Sommerfeld radiation condition, and this is given by Equation (52).
We can now be sure that Equation (50) is the unique solution of
Equation (30), subject to the boundary condition (54). This boundary
condition ensures that infinity is an absorber of electromagnetic radiation, but
not an emitter, which seems entirely reasonable.



Next: Retarded Potentials
Up: Maxwell's Equations
Previous: Three-Dimensional Dirac Delta Function
Richard Fitzpatrick
2014-06-27

![]() can be expressed as a
Fourier integral,
can be expressed as a
Fourier integral,
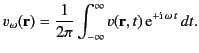
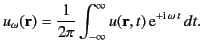
![[*]](footnote.png)
![]() from Equations (33), (38), and
(40), we obtain
from Equations (33), (38), and
(40), we obtain
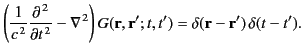
![$\displaystyle G^{(\pm)} ({\bf r}, {\bf r}'; t, t') = \frac{\delta(t'-[t\mp \vert{\bf r}- {\bf r'}\vert/c])}{4\pi \,\vert{\bf r}-{\bf r}'\vert},$](img145.png)
![]() that
appears momentarily at time
that
appears momentarily at time ![]() . According to the retarded Green's
function,
. According to the retarded Green's
function, ![]() , this response consists of a spherical wave, centered
on the point
, this response consists of a spherical wave, centered
on the point ![]() , that propagates forward in time.
In order for the wave to reach position
, that propagates forward in time.
In order for the wave to reach position ![]() at time
at time ![]() , it must
have been emitted from the source at
, it must
have been emitted from the source at ![]() at the retarded
time
at the retarded
time
![]() . According to the
advanced Green's function,
. According to the
advanced Green's function, ![]() , the response consists of a
spherical wave, centered
on the point
, the response consists of a
spherical wave, centered
on the point ![]() , that propagates backward in time. Clearly, the advanced
potential is not consistent with our ideas about causality, which
demand that an effect can never precede its cause in time. Thus, the
Green's function that is consistent with our experience is
, that propagates backward in time. Clearly, the advanced
potential is not consistent with our ideas about causality, which
demand that an effect can never precede its cause in time. Thus, the
Green's function that is consistent with our experience is
![$\displaystyle u({\bf r}, t) = \int \frac{ [v({\bf r}')]} {4\pi\,\vert{\bf r} - {\bf r}'\vert}\,dV',$](img155.png)
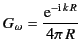
![]() . Let us
call these solutions
. Let us
call these solutions ![]() and
and ![]() , and let us form the difference
, and let us form the difference
![]() . Consider a surface
. Consider a surface ![]() which is a sphere of arbitrarily
small radius centred on the origin. Consider a second surface
which is a sphere of arbitrarily
small radius centred on the origin. Consider a second surface
![]() which is a sphere of arbitrarily large radius centred on the
origin. Let
which is a sphere of arbitrarily large radius centred on the
origin. Let ![]() denote the volume enclosed by these surfaces.
The difference function
denote the volume enclosed by these surfaces.
The difference function ![]() satisfies the homogeneous Helmholtz equation,
satisfies the homogeneous Helmholtz equation,


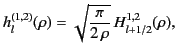
![[*]](footnote.png) It can be demonstrated that
It can be demonstrated that![[*]](footnote.png)
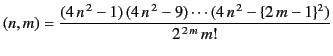
![]() behavior of the
behavior of the
![]() functions is clearly inconsistent
with the Sommerfeld radiation condition, (54). It follows that
all of the
functions is clearly inconsistent
with the Sommerfeld radiation condition, (54). It follows that
all of the ![]() in Equations (61) are zero. The most general solution can
now be expressed in the form
in Equations (61) are zero. The most general solution can
now be expressed in the form
![$\displaystyle {\rm e}^{+{\rm i}\,k\,R} \sum_{n=0,\infty} \left[-\frac{2\,{\rm i...
...n}{R^{\,n+1}} +\frac{n\,(n+1)}{R^{\,n+2}} + \frac{D}{R^{\,n+2}}\right] f_n = 0.$](img195.png)
![$\displaystyle {\rm e}^{+{\rm i}\,k\,R} \sum_{n=0\,\infty} \frac{-2\,{\rm i}\,k\, (n+1) \,f_{n+1} + [n\,(n+1)+D]\,f_n }{R^{\,n+2}} =0,$](img198.png)
![]() , we can replace
, we can replace ![]() by the first term of
its expansion in (66), so that
by the first term of
its expansion in (66), so that