Sound Waves
A sound wave is a type of longitudinal wave that causes a disturbance in the pressure and density of an ideal gas through which it passes.
Consider a plane sound wave propagating in the  -direction.
Let
-direction.
Let 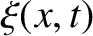 be the longitudinal displacement of the gas associated with the wave. Consider a slab of gas of
cross-sectional area
be the longitudinal displacement of the gas associated with the wave. Consider a slab of gas of
cross-sectional area  lying between
lying between  and
and 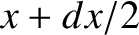 . The mass of the slab is
. The mass of the slab is
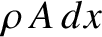 , where
, where 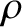 is gas's mass density. The slab's equation of longitudinal motion is
is gas's mass density. The slab's equation of longitudinal motion is
![$\displaystyle \rho\,A\,dx\,\frac{\partial^{2}\xi}{\partial t^{2}} = A\left[-p(x+dx/2)+p(x-dx/2)\right]=-A\,\frac{\partial p}{\partial x}\,dx,$](img3671.png) |
(5.155) |
which gives
 |
(5.156) |
The change in volume of the slab of gas is
![$\displaystyle \delta V = A\left[\xi(x+dx/2)-\xi(x-dx/2)\right]=A\,\frac{\partial\xi}{\partial x}\,dx,$](img3673.png) |
(5.157) |
which yields
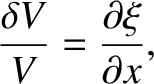 |
(5.158) |
because 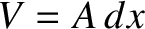 . However,
. However,
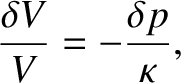 |
(5.159) |
where 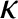 is the bulk modulus. [See Equation (5.146).]
Hence,
is the bulk modulus. [See Equation (5.146).]
Hence,
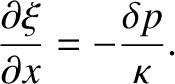 |
(5.160) |
Equation (5.156) gives
 |
(5.161) |
writing
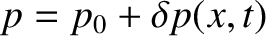 , where
, where 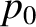 is a constant background pressure.
The previous two equations can be combined to yield
is a constant background pressure.
The previous two equations can be combined to yield
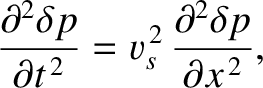 |
(5.162) |
where
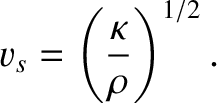 |
(5.163) |
Equation (5.162) is a one-dimensional wave equation that has the standard solution
![$\displaystyle \delta p(x, t)=\delta p_0 \,\cos[k\,(x-v_s\,t)],$](img3682.png) |
(5.164) |
where
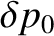 and
and  are constants. The previous solution corresponds to a wave-like
disturbance in the gas pressure of amplitude
are constants. The previous solution corresponds to a wave-like
disturbance in the gas pressure of amplitude
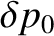 , wavenumber
, wavenumber
 , and
phase velocity
, and
phase velocity 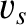 . In other words, Equation (5.163) specifies the speed of sound in an ideal gas.
. In other words, Equation (5.163) specifies the speed of sound in an ideal gas.
It remains to determine whether the compression of the gas associated with the passage of a sound wave is
isothermal or isentropic. In fact, because ideal gases are relatively poor conductors of heat (see Section 5.3.10), the period of vibration
of a sound wave is generally much shorter than the relaxation time necessary for a small
element of the gas to exchange energy with the remainder of the gas by means of heat
flow. Hence, the compression of the gas associated with the passage of a sound wave is isentropic.
It follows from Equations (5.154) and (5.163) that the speed of sound in an ideal gas is
 |
(5.165) |
Making use of Equations (5.97) and (5.129), the previous equation becomes
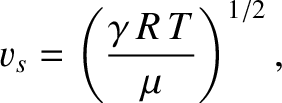 |
(5.166) |
where 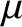 is the molecular mass. Note that the speed of sound in an ideal gas only depends on the
gas temperature, and is independent of the pressure.
is the molecular mass. Note that the speed of sound in an ideal gas only depends on the
gas temperature, and is independent of the pressure.
It is a good approximation to treat the Earth's atmosphere as an ideal gas. The atmosphere is
mostly diatomic, which implies that
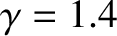 . [See Equation (5.122).] Moreover, the
molecular weight of the atmosphere is
. [See Equation (5.122).] Moreover, the
molecular weight of the atmosphere is
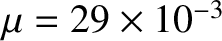 kg. (See Section 5.2.6.) Hence,
the speed of sound in air at
kg. (See Section 5.2.6.) Hence,
the speed of sound in air at 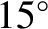 C is
C is
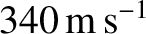 .
.
 -direction.
Let
-direction.
Let 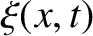 be the longitudinal displacement of the gas associated with the wave. Consider a slab of gas of
cross-sectional area
be the longitudinal displacement of the gas associated with the wave. Consider a slab of gas of
cross-sectional area  lying between
lying between  and
and 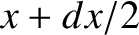 . The mass of the slab is
. The mass of the slab is
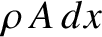 , where
, where 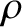 is gas's mass density. The slab's equation of longitudinal motion is
is gas's mass density. The slab's equation of longitudinal motion is
![$\displaystyle \rho\,A\,dx\,\frac{\partial^{2}\xi}{\partial t^{2}} = A\left[-p(x+dx/2)+p(x-dx/2)\right]=-A\,\frac{\partial p}{\partial x}\,dx,$](img3671.png)
![$\displaystyle \delta V = A\left[\xi(x+dx/2)-\xi(x-dx/2)\right]=A\,\frac{\partial\xi}{\partial x}\,dx,$](img3673.png)
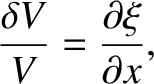
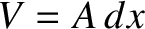 . However,
. However,
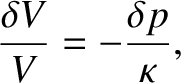
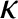 is the bulk modulus. [See Equation (5.146).]
Hence,
is the bulk modulus. [See Equation (5.146).]
Hence,
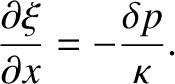

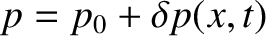 , where
, where 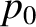 is a constant background pressure.
The previous two equations can be combined to yield
where
is a constant background pressure.
The previous two equations can be combined to yield
where
![$\displaystyle \delta p(x, t)=\delta p_0 \,\cos[k\,(x-v_s\,t)],$](img3682.png)
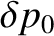 and
and  are constants. The previous solution corresponds to a wave-like
disturbance in the gas pressure of amplitude
are constants. The previous solution corresponds to a wave-like
disturbance in the gas pressure of amplitude
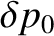 , wavenumber
, wavenumber
 , and
phase velocity
, and
phase velocity 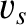 . In other words, Equation (5.163) specifies the speed of sound in an ideal gas.
. In other words, Equation (5.163) specifies the speed of sound in an ideal gas.

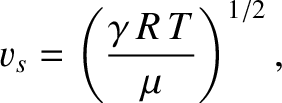
 is the molecular mass. Note that the speed of sound in an ideal gas only depends on the
gas temperature, and is independent of the pressure.
is the molecular mass. Note that the speed of sound in an ideal gas only depends on the
gas temperature, and is independent of the pressure.
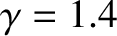 . [See Equation (5.122).] Moreover, the
molecular weight of the atmosphere is
. [See Equation (5.122).] Moreover, the
molecular weight of the atmosphere is
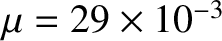 kg. (See Section 5.2.6.) Hence,
the speed of sound in air at
kg. (See Section 5.2.6.) Hence,
the speed of sound in air at 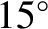 C is
C is
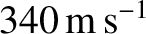 .
.