Next: Isothermal Atmosphere Up: Ideal Gas Previous: Isothermal and Adiabatic Expansion
Let us, first of all, consider the hydrostatic equilibrium of the atmosphere.
Consider a thin vertical slice
of the atmosphere, of cross-sectional area  , that starts at height
, that starts at height  above
ground level, and extends to
height
above
ground level, and extends to
height 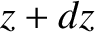 . The upward force exerted on this slice by the gas below it
is
. The upward force exerted on this slice by the gas below it
is 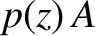 , where
, where 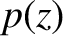 is the pressure at height
is the pressure at height  .
Likewise, the downward force exerted by the gas above the slice is
.
Likewise, the downward force exerted by the gas above the slice is
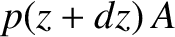 . The net upward force is
. The net upward force is
![$[p(z) - p(z+dz)]\,A$](img3595.png) . In equilibrium,
this upward force must be balanced by the downward force due to the weight of
the slice, which is
. In equilibrium,
this upward force must be balanced by the downward force due to the weight of
the slice, which is
 , where
, where 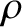 is the mass density of
the gas, and
is the mass density of
the gas, and 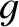 the acceleration due to gravity. It follows that the
force balance condition can be written
the acceleration due to gravity. It follows that the
force balance condition can be written
![$\displaystyle [p(z)- p(z+dz)]\,A = \rho \,A\,dz\,g,$](img3597.png) |
(5.127) |
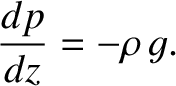 |
(5.128) |
We can express the mass density of a gas in the following form,
where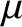 is the molecular weight of the gas,
and is equal to the mass of one mole of gas particles.
For instance, the molecular weight of nitrogen gas is
is the molecular weight of the gas,
and is equal to the mass of one mole of gas particles.
For instance, the molecular weight of nitrogen gas is
 kg.
The previous formula for the mass density of a gas,
combined with the ideal gas law,
kg.
The previous formula for the mass density of a gas,
combined with the ideal gas law,
 , yields
It follows that the equation of hydrostatic equilibrium can be rewritten
, yields
It follows that the equation of hydrostatic equilibrium can be rewritten