The bulk modulus of an ideal gas is a measure of its resistance to bulk compression, and
is defined
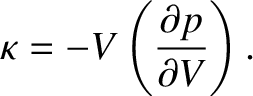 |
(5.146) |
In fact, an ideal gas possesses a number of different bulk moduli depending on what is
held constant as the pressure is varied. The two most important bulk moduli are the
isothermal bulk modulus,
 |
(5.147) |
and the isentropic bulk modulus,
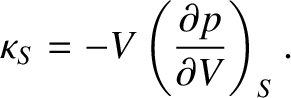 |
(5.148) |
The former describes situations in which the gas undergoes isothermal compression, whereas the
latter describes situations in which the gas undergoes adiabatic compression. (Note that  actually denotes entropy.
However, a gas that undergoes compression at constant entropy is such that no heat is added to the gas during the compression.)
actually denotes entropy.
However, a gas that undergoes compression at constant entropy is such that no heat is added to the gas during the compression.)
According to the isothermal gas law, (5.114),
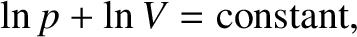 |
(5.149) |
so
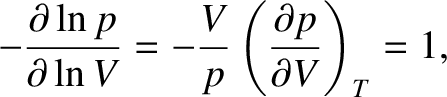 |
(5.150) |
which implies that
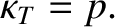 |
(5.151) |
According to the adiabatic gas law, (5.124),
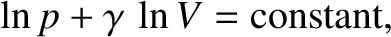 |
(5.152) |
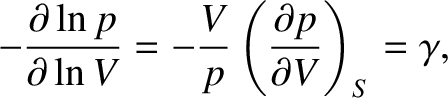 |
(5.153) |
which implies that
 |
(5.154) |
Note that the isentropic bulk modulus of an ideal gas is greater than its isothermal bulk modulus (because 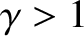 ). In other words, an ideal gas resists adiabatic compression to a greater degree than it resists
isothermal compression. This is the case because during adiabatic compression the work done on the
gas causes its temperature to rise, leading to a greater increase in the pressure than would be obtained if
the temperature were held constant.
). In other words, an ideal gas resists adiabatic compression to a greater degree than it resists
isothermal compression. This is the case because during adiabatic compression the work done on the
gas causes its temperature to rise, leading to a greater increase in the pressure than would be obtained if
the temperature were held constant.

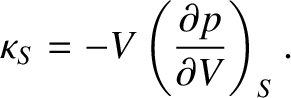
 actually denotes entropy.
However, a gas that undergoes compression at constant entropy is such that no heat is added to the gas during the compression.)
actually denotes entropy.
However, a gas that undergoes compression at constant entropy is such that no heat is added to the gas during the compression.)
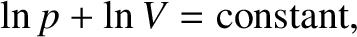
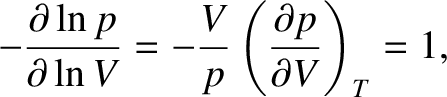
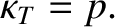
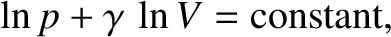
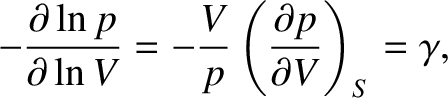
 ). In other words, an ideal gas resists adiabatic compression to a greater degree than it resists
isothermal compression. This is the case because during adiabatic compression the work done on the
gas causes its temperature to rise, leading to a greater increase in the pressure than would be obtained if
the temperature were held constant.
). In other words, an ideal gas resists adiabatic compression to a greater degree than it resists
isothermal compression. This is the case because during adiabatic compression the work done on the
gas causes its temperature to rise, leading to a greater increase in the pressure than would be obtained if
the temperature were held constant.