Adiabatic Atmosphere
Of course, we know that the atmosphere is not isothermal. In fact, air
temperature falls quite noticeably with
increasing altitude. In ski resorts, the general rule of thumb is that the temperature drops by about 1 degree per 100 meters increase in altitude.
Many people cannot understand
why the atmosphere gets colder with increasing height. They reason that because higher altitudes
are closer to the Sun they ought to be hotter.
In fact, the explanation is quite
simple. It depends on three important properties of air. The first
property is that air is transparent to most, but by no means all, of the
electromagnetic spectrum. In particular, most infrared radiation, which carries heat
energy, passes straight through the lower atmosphere, and heats the ground. In other
words, the lower atmosphere is heated from below, not from above. The
second important
property of air is that it is constantly in motion. In fact, the lower 20 kilometers
of the atmosphere (the so-called troposphere)
are fairly thoroughly mixed. You might think that this
would imply that the atmosphere is
isothermal. However, this is not the case because of
the final important property of air; namely, it is a very poor conductor of heat. (See Section 5.3.10.)
This, of course, is why woolly sweaters work; they trap a layer of air close to
the body, and, because air is such a poor conductor of heat, you stay warm.
Imagine a packet of air that is swirling around in the atmosphere. We would
expect it to always remain at the same pressure as its surroundings, otherwise it
would be mechanically unstable. It is also plausible that the packet moves around
too quickly to effectively exchange heat with its surroundings, because
air is very a poor heat conductor, and heat flow is consequently quite a
slow process. So,
to a first approximation, the air in the packet is adiabatic.
In a steady-state atmosphere, we expect that, as the packet moves upwards,
expands due to the reduced pressure, and cools adiabatically, its temperature
always remains the same as that of its immediate surroundings.
This implies that we
can use the adiabatic gas law to characterize the cooling of the
atmosphere with increasing altitude. In this particular
case, the most useful manifestation of the adiabatic law is
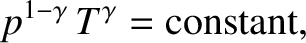 |
(5.134) |
giving
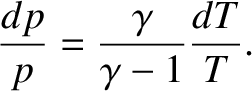 |
(5.135) |
Combining the previous expression with the equation of hydrostatic equilibrium,
(5.131), we obtain
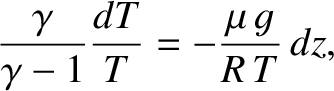 |
(5.136) |
or
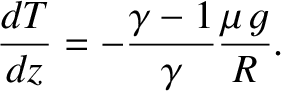 |
(5.137) |
Now, the ratio of specific heats for air (which is effectively
a diatomic gas) is about 1.4. [See Equation (5.122).]
Hence, given that
 and
and
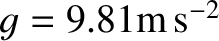 , we deduce, from the
previous expression, that the temperature of the atmosphere decreases with
increasing height
at a constant rate of
, we deduce, from the
previous expression, that the temperature of the atmosphere decreases with
increasing height
at a constant rate of 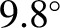 C per kilometer.
This value is called the (dry) adiabatic lapse rate of the atmosphere.
Our calculation accords well with the
“
C per kilometer.
This value is called the (dry) adiabatic lapse rate of the atmosphere.
Our calculation accords well with the
“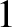 degree colder per 100 meters higher” rule of thumb used in ski resorts.
The basic reason that air is colder at higher altitudes is
that it expands as its pressure decreases with height. It, therefore, does work
on its environment, without absorbing any heat (because of its low thermal
conductivity),
so its internal energy, and, hence, its temperature decreases.
degree colder per 100 meters higher” rule of thumb used in ski resorts.
The basic reason that air is colder at higher altitudes is
that it expands as its pressure decreases with height. It, therefore, does work
on its environment, without absorbing any heat (because of its low thermal
conductivity),
so its internal energy, and, hence, its temperature decreases.
According to the adiabatic lapse rate calculated previously, the air temperature at
the cruising altitude of airliners (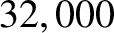 feet) should be about
feet) should be about 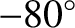 C
(assuming a sea level temperature of
C
(assuming a sea level temperature of 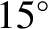 C).
In fact, this is somewhat of an underestimate. A more realistic value is about
C).
In fact, this is somewhat of an underestimate. A more realistic value is about
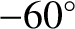 C.
The explanation for this
discrepancy is the presence of
water vapor in the atmosphere. As air rises, expands, and cools, water
vapor condenses out, releasing latent heat, which prevents the temperature
from falling as rapidly with height as the adiabatic lapse rate would predict.
In fact, in the tropics, where the air humidity is very high, the lapse rate of
the atmosphere (i.e., the rate of decrease of temperature with altitude)
is significantly less than the adiabatic value. The adiabatic
lapse rate is only observed when the humidity is low. This is the case in deserts,
in the arctic (where water vapor is frozen out of the atmosphere), and, of course,
in ski resorts.
C.
The explanation for this
discrepancy is the presence of
water vapor in the atmosphere. As air rises, expands, and cools, water
vapor condenses out, releasing latent heat, which prevents the temperature
from falling as rapidly with height as the adiabatic lapse rate would predict.
In fact, in the tropics, where the air humidity is very high, the lapse rate of
the atmosphere (i.e., the rate of decrease of temperature with altitude)
is significantly less than the adiabatic value. The adiabatic
lapse rate is only observed when the humidity is low. This is the case in deserts,
in the arctic (where water vapor is frozen out of the atmosphere), and, of course,
in ski resorts.
Suppose that the lapse rate of the atmosphere differs from the adiabatic value.
Let us ignore the complication of water vapor, and assume that the atmosphere
is dry. Consider a packet of air that moves slightly upwards
from its equilibrium height. The temperature of the packet will
decrease with altitude according to the adiabatic lapse rate, because its
expansion is adiabatic. We shall assume that the packet always maintains pressure
balance with its surroundings. It follows that because
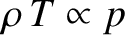 ,
according to the ideal gas law,
,
according to the ideal gas law,
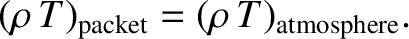 |
(5.138) |
If the atmospheric lapse rate is less than the adiabatic value then
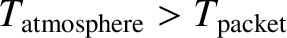 implying that
implying that
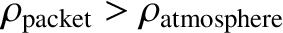 . So, the packet will be denser than its immediate
surroundings, and will, therefore, tend to fall back to its original height.
Clearly, an atmosphere whose lapse rate is less than the adiabatic value is
vertically stable. On the other hand, if the atmospheric lapse rate exceeds the adiabatic
value then, after rising a little way,
the packet will be less dense than its immediate surroundings, and will, therefore,
continue to rise due to buoyancy effects.
Clearly, an atmosphere whose lapse rate is greater
than the adiabatic value is vertically unstable. This effect is of great importance
in meteorology. The normal stable state of the atmosphere is for the lapse rate
to be slightly less than
the adiabatic value. Occasionally, however, the lapse rate exceeds
the adiabatic value, and this is always associated with
extremely disturbed weather patterns.
. So, the packet will be denser than its immediate
surroundings, and will, therefore, tend to fall back to its original height.
Clearly, an atmosphere whose lapse rate is less than the adiabatic value is
vertically stable. On the other hand, if the atmospheric lapse rate exceeds the adiabatic
value then, after rising a little way,
the packet will be less dense than its immediate surroundings, and will, therefore,
continue to rise due to buoyancy effects.
Clearly, an atmosphere whose lapse rate is greater
than the adiabatic value is vertically unstable. This effect is of great importance
in meteorology. The normal stable state of the atmosphere is for the lapse rate
to be slightly less than
the adiabatic value. Occasionally, however, the lapse rate exceeds
the adiabatic value, and this is always associated with
extremely disturbed weather patterns.
Let us consider the temperature, pressure, and density profiles in an
adiabatic atmosphere. We can directly integrate Equation (5.137) to
give
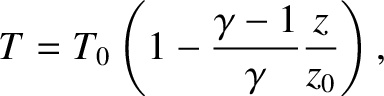 |
(5.139) |
where 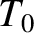 is the ground-level temperature, and
is the ground-level temperature, and
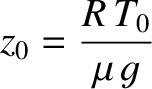 |
(5.140) |
the isothermal scale-height calculated using this temperature. The
pressure profile is easily calculated from the adiabatic gas law
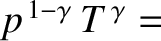 constant, or
constant, or
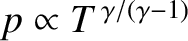 . It
follows that
. It
follows that
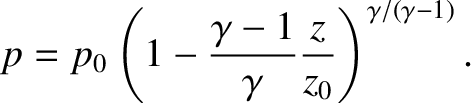 |
(5.141) |
Consider the limit
 . In this limit, Equation (5.139) yields
. In this limit, Equation (5.139) yields
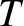 independent of height (i.e., the atmosphere becomes isothermal). We can evaluate
Equation (5.141) in the limit
as
independent of height (i.e., the atmosphere becomes isothermal). We can evaluate
Equation (5.141) in the limit
as
 using the mathematical identity
using the mathematical identity
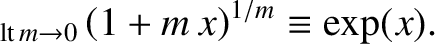 |
(5.142) |
We obtain
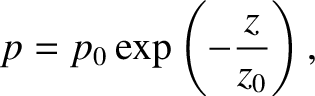 |
(5.143) |
which, not surprisingly, is the predicted pressure variation
in an isothermal atmosphere. In reality,
the ratio of specific heats of the atmosphere is not unity, but is about 1.4
(i.e., the ratio for diatomic gases), which
implies that in the real atmosphere
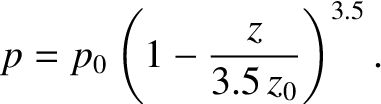 |
(5.144) |
In fact, this formula gives very similar results to the isothermal formula,
Equation (5.143), for heights below one scale-height (i.e., 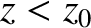 ). For heights
above one scale-height, the isothermal formula tends to predict too high
a pressure. See Figure 5.1. So, in an adiabatic atmosphere, the pressure falls off more quickly
with altitude than in an isothermal atmosphere, but this effect is only
noticeable at pressures significantly below one atmosphere. In fact, the isothermal
formula is a fairly good approximation below altitudes of about 10 kilometers.
Because
). For heights
above one scale-height, the isothermal formula tends to predict too high
a pressure. See Figure 5.1. So, in an adiabatic atmosphere, the pressure falls off more quickly
with altitude than in an isothermal atmosphere, but this effect is only
noticeable at pressures significantly below one atmosphere. In fact, the isothermal
formula is a fairly good approximation below altitudes of about 10 kilometers.
Because
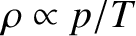 , the variation of density with height is
, the variation of density with height is
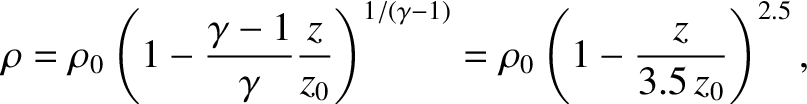 |
(5.145) |
where 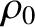 is the density at ground level. Thus, the density falls off
more rapidly with altitude than the temperature, but less rapidly than the
pressure.
is the density at ground level. Thus, the density falls off
more rapidly with altitude than the temperature, but less rapidly than the
pressure.
Figure 5.1:
The solid curve shows the variation of pressure (normalized to the pressure at ground level) with altitude
(normalized to the isothermal scale-height at ground level) in an isothermal atmosphere. The dashed curve shows the
variation of pressure with altitude in an adiabatic atmosphere.
|
|
Note that an adiabatic atmosphere has a sharp upper boundary. Above height
![$z_1 = [\gamma/(\gamma-1)]\,z_0$](img3654.png) , the temperature, pressure, and density are
all zero. In other words, there is no atmosphere. For real air, with
, the temperature, pressure, and density are
all zero. In other words, there is no atmosphere. For real air, with
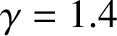 , the upper boundary of an adiabatic atmosphere lies at height
, the upper boundary of an adiabatic atmosphere lies at height
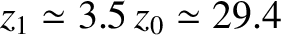 kilometers above sea level. This behavior is quite different
to that of an isothermal atmosphere, which has a diffuse upper boundary. In reality,
there is no sharp upper boundary to the atmosphere. The adiabatic gas law
does not apply above about 20 kilometers (i.e., in the stratosphere) because,
at these altitudes, the air is no longer strongly mixed. Thus, in the stratosphere,
the pressure falls off exponentially with increasing height.
kilometers above sea level. This behavior is quite different
to that of an isothermal atmosphere, which has a diffuse upper boundary. In reality,
there is no sharp upper boundary to the atmosphere. The adiabatic gas law
does not apply above about 20 kilometers (i.e., in the stratosphere) because,
at these altitudes, the air is no longer strongly mixed. Thus, in the stratosphere,
the pressure falls off exponentially with increasing height.
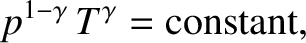
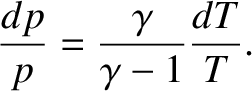
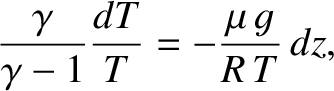
 and
and
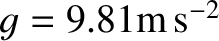 , we deduce, from the
previous expression, that the temperature of the atmosphere decreases with
increasing height
at a constant rate of
, we deduce, from the
previous expression, that the temperature of the atmosphere decreases with
increasing height
at a constant rate of 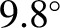 C per kilometer.
This value is called the (dry) adiabatic lapse rate of the atmosphere.
Our calculation accords well with the
“
C per kilometer.
This value is called the (dry) adiabatic lapse rate of the atmosphere.
Our calculation accords well with the
“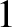 degree colder per 100 meters higher” rule of thumb used in ski resorts.
The basic reason that air is colder at higher altitudes is
that it expands as its pressure decreases with height. It, therefore, does work
on its environment, without absorbing any heat (because of its low thermal
conductivity),
so its internal energy, and, hence, its temperature decreases.
degree colder per 100 meters higher” rule of thumb used in ski resorts.
The basic reason that air is colder at higher altitudes is
that it expands as its pressure decreases with height. It, therefore, does work
on its environment, without absorbing any heat (because of its low thermal
conductivity),
so its internal energy, and, hence, its temperature decreases.
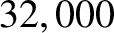 feet) should be about
feet) should be about 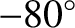 C
(assuming a sea level temperature of
C
(assuming a sea level temperature of 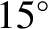 C).
In fact, this is somewhat of an underestimate. A more realistic value is about
C).
In fact, this is somewhat of an underestimate. A more realistic value is about
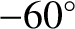 C.
The explanation for this
discrepancy is the presence of
water vapor in the atmosphere. As air rises, expands, and cools, water
vapor condenses out, releasing latent heat, which prevents the temperature
from falling as rapidly with height as the adiabatic lapse rate would predict.
In fact, in the tropics, where the air humidity is very high, the lapse rate of
the atmosphere (i.e., the rate of decrease of temperature with altitude)
is significantly less than the adiabatic value. The adiabatic
lapse rate is only observed when the humidity is low. This is the case in deserts,
in the arctic (where water vapor is frozen out of the atmosphere), and, of course,
in ski resorts.
C.
The explanation for this
discrepancy is the presence of
water vapor in the atmosphere. As air rises, expands, and cools, water
vapor condenses out, releasing latent heat, which prevents the temperature
from falling as rapidly with height as the adiabatic lapse rate would predict.
In fact, in the tropics, where the air humidity is very high, the lapse rate of
the atmosphere (i.e., the rate of decrease of temperature with altitude)
is significantly less than the adiabatic value. The adiabatic
lapse rate is only observed when the humidity is low. This is the case in deserts,
in the arctic (where water vapor is frozen out of the atmosphere), and, of course,
in ski resorts.
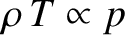 ,
according to the ideal gas law,
,
according to the ideal gas law,
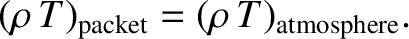
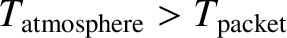 implying that
implying that
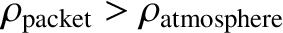 . So, the packet will be denser than its immediate
surroundings, and will, therefore, tend to fall back to its original height.
Clearly, an atmosphere whose lapse rate is less than the adiabatic value is
vertically stable. On the other hand, if the atmospheric lapse rate exceeds the adiabatic
value then, after rising a little way,
the packet will be less dense than its immediate surroundings, and will, therefore,
continue to rise due to buoyancy effects.
Clearly, an atmosphere whose lapse rate is greater
than the adiabatic value is vertically unstable. This effect is of great importance
in meteorology. The normal stable state of the atmosphere is for the lapse rate
to be slightly less than
the adiabatic value. Occasionally, however, the lapse rate exceeds
the adiabatic value, and this is always associated with
extremely disturbed weather patterns.
. So, the packet will be denser than its immediate
surroundings, and will, therefore, tend to fall back to its original height.
Clearly, an atmosphere whose lapse rate is less than the adiabatic value is
vertically stable. On the other hand, if the atmospheric lapse rate exceeds the adiabatic
value then, after rising a little way,
the packet will be less dense than its immediate surroundings, and will, therefore,
continue to rise due to buoyancy effects.
Clearly, an atmosphere whose lapse rate is greater
than the adiabatic value is vertically unstable. This effect is of great importance
in meteorology. The normal stable state of the atmosphere is for the lapse rate
to be slightly less than
the adiabatic value. Occasionally, however, the lapse rate exceeds
the adiabatic value, and this is always associated with
extremely disturbed weather patterns.
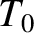 is the ground-level temperature, and
is the ground-level temperature, and
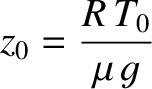
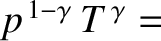 constant, or
constant, or
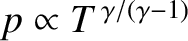 . It
follows that
Consider the limit
. It
follows that
Consider the limit
 . In this limit, Equation (5.139) yields
. In this limit, Equation (5.139) yields
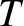 independent of height (i.e., the atmosphere becomes isothermal). We can evaluate
Equation (5.141) in the limit
as
independent of height (i.e., the atmosphere becomes isothermal). We can evaluate
Equation (5.141) in the limit
as
 using the mathematical identity
using the mathematical identity
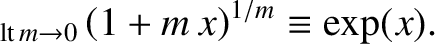
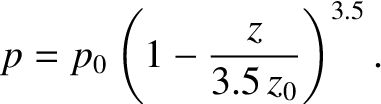
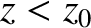 ). For heights
above one scale-height, the isothermal formula tends to predict too high
a pressure. See Figure 5.1. So, in an adiabatic atmosphere, the pressure falls off more quickly
with altitude than in an isothermal atmosphere, but this effect is only
noticeable at pressures significantly below one atmosphere. In fact, the isothermal
formula is a fairly good approximation below altitudes of about 10 kilometers.
Because
). For heights
above one scale-height, the isothermal formula tends to predict too high
a pressure. See Figure 5.1. So, in an adiabatic atmosphere, the pressure falls off more quickly
with altitude than in an isothermal atmosphere, but this effect is only
noticeable at pressures significantly below one atmosphere. In fact, the isothermal
formula is a fairly good approximation below altitudes of about 10 kilometers.
Because
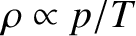 , the variation of density with height is
, the variation of density with height is
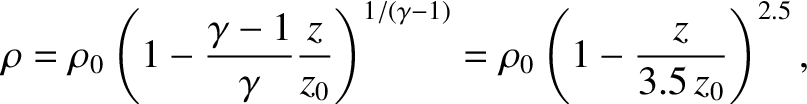
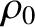 is the density at ground level. Thus, the density falls off
more rapidly with altitude than the temperature, but less rapidly than the
pressure.
is the density at ground level. Thus, the density falls off
more rapidly with altitude than the temperature, but less rapidly than the
pressure.
![\includegraphics[width=.85\textwidth]{Chapter06/air.eps}](img3653.png)
![$z_1 = [\gamma/(\gamma-1)]\,z_0$](img3654.png) , the temperature, pressure, and density are
all zero. In other words, there is no atmosphere. For real air, with
, the temperature, pressure, and density are
all zero. In other words, there is no atmosphere. For real air, with
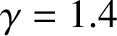 , the upper boundary of an adiabatic atmosphere lies at height
, the upper boundary of an adiabatic atmosphere lies at height
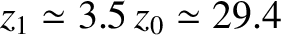 kilometers above sea level. This behavior is quite different
to that of an isothermal atmosphere, which has a diffuse upper boundary. In reality,
there is no sharp upper boundary to the atmosphere. The adiabatic gas law
does not apply above about 20 kilometers (i.e., in the stratosphere) because,
at these altitudes, the air is no longer strongly mixed. Thus, in the stratosphere,
the pressure falls off exponentially with increasing height.
kilometers above sea level. This behavior is quite different
to that of an isothermal atmosphere, which has a diffuse upper boundary. In reality,
there is no sharp upper boundary to the atmosphere. The adiabatic gas law
does not apply above about 20 kilometers (i.e., in the stratosphere) because,
at these altitudes, the air is no longer strongly mixed. Thus, in the stratosphere,
the pressure falls off exponentially with increasing height.