Next: Light Waves in a Up: Experimental Basis of Special Previous: Experimental Basis of Special
 is the gas's ratio of specific heats (which is approximately 1.4 for the atmosphere),
is the gas's ratio of specific heats (which is approximately 1.4 for the atmosphere),
 the gas's undisturbed pressure, and
the gas's undisturbed pressure, and 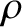 the gas's undisturbed mass density.
Note that a sound wave is a non-dispersive wave, which means that a transient wave pulse propagates at the same speed as an infinite wave train. (See Section 4.2.6.)
However, a sound wave only propagates at the speed (3.1) in the rest frame of the gas.
the gas's undisturbed mass density.
Note that a sound wave is a non-dispersive wave, which means that a transient wave pulse propagates at the same speed as an infinite wave train. (See Section 4.2.6.)
However, a sound wave only propagates at the speed (3.1) in the rest frame of the gas.
Let 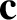 be the phase velocity of a sound wave in a stationary frame of reference in which the
gas is at rest. Thus,
be the phase velocity of a sound wave in a stationary frame of reference in which the
gas is at rest. Thus,
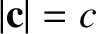 , is the speed of sound, (3.1). Consider a moving frame of reference that moves at constant velocity
, is the speed of sound, (3.1). Consider a moving frame of reference that moves at constant velocity  , where
, where  ,
with respect to the stationary frame. Incidentally, if the stationary frame is inertial then so is the moving frame.
(See Section 1.5.4.) The gas appears to flow with uniform velocity
,
with respect to the stationary frame. Incidentally, if the stationary frame is inertial then so is the moving frame.
(See Section 1.5.4.) The gas appears to flow with uniform velocity 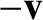 in the moving reference frame.
Furthermore, it is an experimentally
verified fact that the sound wave appears to propagate with the phase velocity
in the moving reference frame.
Furthermore, it is an experimentally
verified fact that the sound wave appears to propagate with the phase velocity
 |
(3.3) |
 in the moving
frame then it propagates at the speed
but if the sound wave propagates in the opposite direction to
in the moving
frame then it propagates at the speed
but if the sound wave propagates in the opposite direction to  in the moving frame then it propagates
at the speed
and, finally, if the sound wave propagates in a direction perpendicular to
in the moving frame then it propagates
at the speed
and, finally, if the sound wave propagates in a direction perpendicular to  in the moving frame then it propagates at the
speed
in the moving frame then it propagates at the
speed
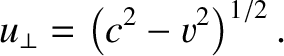 |
(3.6) |
 in all
directions in the stationary frame. These ideas are illustrated in Figure 3.1.
in all
directions in the stationary frame. These ideas are illustrated in Figure 3.1.
We could imagine performing an experiment in the moving reference frame in order to measure its
velocity,  , with respect to the stationary frame. See Figure 3.2. Suppose that we have a sound wave source that
emits a transient sound wave pulse isotropically in all directions. Suppose that we place two small sound-wave reflectors
(which are stationary in the moving frame) at equal distances
, with respect to the stationary frame. See Figure 3.2. Suppose that we have a sound wave source that
emits a transient sound wave pulse isotropically in all directions. Suppose that we place two small sound-wave reflectors
(which are stationary in the moving frame) at equal distances 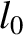 from the source. The displacement of the first reflector from the source is in the direction of
from the source. The displacement of the first reflector from the source is in the direction of  , whereas the displacement of the second reflector is in a direction that is perpendicular to
, whereas the displacement of the second reflector is in a direction that is perpendicular to  . The travel time of the pulse from the source to the first reflector, and back
again, is
. The travel time of the pulse from the source to the first reflector, and back
again, is
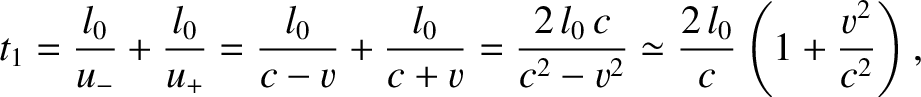 |
(3.7) |
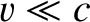 .
The travel time of the pulse from the source to the second reflector, and back again, is
.
The travel time of the pulse from the source to the second reflector, and back again, is
 |
(3.8) |
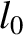 and
and  , we can determine
, we can determine  . We can also determine the direction of
. We can also determine the direction of
 because the time difference is maximized when the two legs of the apparatus shown in Figure 3.2 are
aligned parallel and perpendicular to this direction.
because the time difference is maximized when the two legs of the apparatus shown in Figure 3.2 are
aligned parallel and perpendicular to this direction.