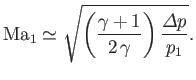Next: Piston-Generated Shock Wave
Up: One-Dimensional Compressible Inviscid Flow
Previous: Sonic Flow through a
Normal Shocks
As previously described, there is an effective discontinuity in the flow speed, pressure, density, and temperature, of the
gas flowing through the diverging part of an over-expanded Laval nozzle. This type of discontinuity is known as a
normal shock. Let us investigate the properties of such shocks.
Our fundamental equations are the mass conservation equation [see Equation (14.30)],
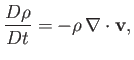 |
(14.80) |
the momentum conservation equation [see Equation (14.31)],
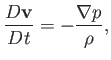 |
(14.81) |
and the energy conservation equation [see Equation (1.75)],
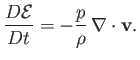 |
(14.82) |
In writing the previous equations, we have neglected viscosity, heat conduction, and potential energy.
Note that we have used the more fundamental energy conservation equation, (1.75), rather than Equation (14.32), because the latter equation incorporates the ideal
gas law, and this law is not valid inside the shock, because the gas there is not in thermodynamic equilibrium.
Consider a compressible gas flowing steadily down a duct of constant cross-sectional area  . Let
. Let  measure distance along the duct. The
gas's temperature,
measure distance along the duct. The
gas's temperature, 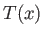 , density,
, density, 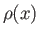 , pressure
, pressure 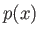 , specific internal energy
, specific internal energy
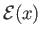 , and normal velocity
, and normal velocity 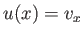 , are all assumed to be constant across any
cross-section, and independent of time. Let the shock be situated at
, are all assumed to be constant across any
cross-section, and independent of time. Let the shock be situated at  . Suppose that in the region upstream of the shock,
. Suppose that in the region upstream of the shock, 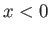 , the temperature, density, pressure, specific internal energy, and
flow speed of the gas take the constant values
, the temperature, density, pressure, specific internal energy, and
flow speed of the gas take the constant values 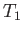 ,
, 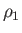 ,
, 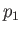 ,
,
 , and
, and 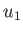 , respectively. Likewise, suppose that in the region
downstream of the shock,
, respectively. Likewise, suppose that in the region
downstream of the shock,  , the temperature, density, pressure, specific internal energy, and
flow speed of the gas take the constant values
, the temperature, density, pressure, specific internal energy, and
flow speed of the gas take the constant values  ,
, 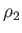 ,
,  ,
,
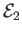 , and
, and 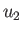 , respectively. Of course, in the immediate
vicinity of the shock,
, respectively. Of course, in the immediate
vicinity of the shock, 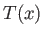 ,
, 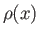 ,
, 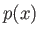 ,
,
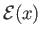 , and
, and 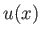 are all rapidly-varying functions of
are all rapidly-varying functions of  . We wish to find the
relationship between the upstream and downstream gas parameters. We can achieve this goal by invoking conservation of mass,
momentum, and energy across the shock--in other words, by making use of Equations (14.80)-(14.82).
. We wish to find the
relationship between the upstream and downstream gas parameters. We can achieve this goal by invoking conservation of mass,
momentum, and energy across the shock--in other words, by making use of Equations (14.80)-(14.82).
The mass continuity equation (14.71) yields
 |
(14.83) |
which can be rearranged to give
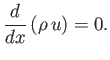 |
(14.84) |
The momentum conservation equation (14.72) yields
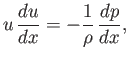 |
(14.85) |
which can be rearranged to give
 |
(14.86) |
or
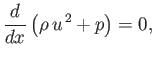 |
(14.87) |
where use has been made of Equation (14.84).
Finally, the energy conservation equation (14.73) yields
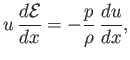 |
(14.88) |
which can be rearranged to give
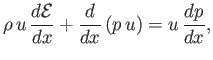 |
(14.89) |
or
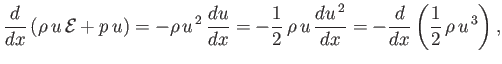 |
(14.90) |
where use has been made of Equations (14.84) and (14.86).
Thus, we obtain
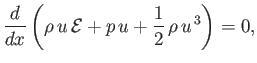 |
(14.91) |
which reduces to
 |
(14.92) |
with the aid of Equation (14.84). The previous equation can also be written
 |
(14.93) |
where
 is the specific enthalpy of the gas. [See Equation (14.18).]
is the specific enthalpy of the gas. [See Equation (14.18).]
Integrating Equations (14.84), (14.87), and (14.93) across the shock, we obtain
where
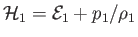 , et cetera. We shall assume that the gas
upstream and downstream of the shock obeys the ideal gas law, and has the same ratio
of specific heats,
, et cetera. We shall assume that the gas
upstream and downstream of the shock obeys the ideal gas law, and has the same ratio
of specific heats, 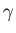 . It follows that
. It follows that
where use has been made of Equations (14.1), (14.18), and (14.60).
Let
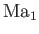 and
and
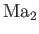 be the Mach numbers upstream and downstream of the shock, respectively.
Thus,
be the Mach numbers upstream and downstream of the shock, respectively.
Thus,
 |
(14.99) |
where use has been made of Equations (14.45) and (14.57). Equations (14.96), (14.98), and
(14.99) can be combined to give
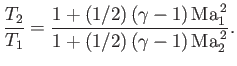 |
(14.100) |
Equations (14.94) and (14.99) yield
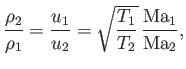 |
(14.101) |
or
 |
(14.102) |
where use has been made of Equation (14.97). Finally, Equations (14.95), (14.97),
and (14.99) give
 |
(14.103) |
Eliminating  ,
, 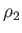 , and
, and  between Equations (14.100), (14.101), and
(14.103), we obtain
between Equations (14.100), (14.101), and
(14.103), we obtain
![$\displaystyle {\rm Ma}_2=\left[\frac{2+(\gamma-1)\,{\rm Ma}_1^{\,2}}{1-\gamma+2\,\gamma\,{\rm Ma}_1^{\,2}}\right]^{1/2}.$](img5478.png) |
(14.104) |
Note that
 |
(14.105) |
Moreover, it is easily verified that
 when
when
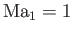 . Hence, we deduce that
. Hence, we deduce that
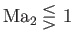 as as 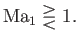 |
(14.106) |
In other words, if the downstream flow is subsonic then the upstream flow is supersonic, and vice versa.
Equations (14.1), (14.100), (14.101), (14.103), and (14.104) can be
combined to give
The previous three equations completely describe the conditions downstream of the shock in terms of the upstream conditions. We can rearrange
these equations to give
The latter two equations are known as the Rankine-Hugoniot relations.
According to Equation (14.25), the jump in specific entropy across the shock is
![$\displaystyle {\cal S}_2-{\cal S}_1={\cal C}_V\ln\left[\frac{p_2}{p_1}\left(\frac{\rho_1}{\rho_2}\right)^\gamma\right].$](img5493.png) |
(14.113) |
It follows from Equations (14.107) and (14.108) that
![$\displaystyle {\cal S}_2-{\cal S}_1 = {\cal C}_V\ln\left[G({\rm Ma}_1^{\,2})\right],$](img5494.png) |
(14.114) |
where
![$\displaystyle G(x) = \left(\frac{1-\gamma+2\,\gamma\,x}{\gamma+1}\right)\left[\frac{2+(\gamma-1)\,x}{(\gamma+1)\,x}\right]^{\,\gamma}.$](img5495.png) |
(14.115) |
It is easily demonstrated that
![$\displaystyle \frac{dG}{dx} = 2\,\gamma\,(\gamma-1)\,(1-x)^{\,2}\,\frac{[2+(\gamma-1)\,x]^{\,\gamma-1}}{[(\gamma+1)\,x]^{\,\gamma+1}}\geq 0.$](img5496.png) |
(14.116) |
Moreover, 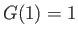 . Hence, we deduce that
. Hence, we deduce that
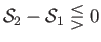 as as 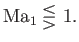 |
(14.117) |
Now, the second law of thermodynamics forbids a spontaneous decrease in the specific entropy
of the gas as it passes through the shock (Reif 1965). In other words, the second law of thermodynamics demands that
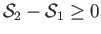 . It follows that
. It follows that
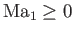 . However, it is easily seen from Equations (14.107)-(14.109)
that
. However, it is easily seen from Equations (14.107)-(14.109)
that
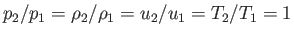 when
when
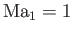 . In other words, there is no shock (i.e., no discontinuity in the
properties of the gas at
. In other words, there is no shock (i.e., no discontinuity in the
properties of the gas at  ) when the upstream Mach number is exactly unity. Thus, we conclude that the only type of normal
shock that is consistent with the second law of thermodynamics is one in which the upstream flow is supersonic, and the
downstream flow subsonic--that is,
) when the upstream Mach number is exactly unity. Thus, we conclude that the only type of normal
shock that is consistent with the second law of thermodynamics is one in which the upstream flow is supersonic, and the
downstream flow subsonic--that is,
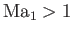 and
and
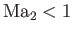 . It is apparent from Equations (14.107)-(14.109)
that if
. It is apparent from Equations (14.107)-(14.109)
that if
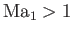 then
then 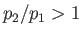 ,
,
 , and
, and 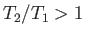 . In other words, the passage of the gas through the shock
front leads to both compression and heating.
. In other words, the passage of the gas through the shock
front leads to both compression and heating.
The dimensionless parameter
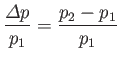 |
(14.118) |
is a convenient measure of shock strength. Thus, a shock is said to be weak if
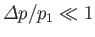 , and
strong if
, and
strong if
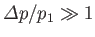 .
.
Consider a weak shock. According to Equations (14.111), (14.112),
(14.114), and (14.116),
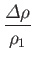 |
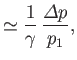 |
(14.119) |
 |
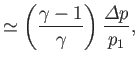 |
(14.120) |
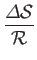 |
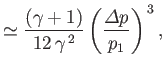 |
(14.121) |
where
 , et cetera, and use has been made of Equation (14.59). It
can be seen that the flow across the shock is isentropic (i.e.,
, et cetera, and use has been made of Equation (14.59). It
can be seen that the flow across the shock is isentropic (i.e.,
 and
and
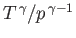 are
constant) to first order in the shock strength. This is the case because the increase in specific entropy across the shock is only third order in the shock strength.
are
constant) to first order in the shock strength. This is the case because the increase in specific entropy across the shock is only third order in the shock strength.
Consider a strong shock. It can be seen from Equations (14.111) and (14.112) that
as
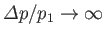 . Clearly, there is a finite limit to the degree of compression of gas passing through a strong shock.
Thus, in the case of a strong shock, the large increase in the pressure across the shock front is predominately caused by a large increase in the
temperature. In other words, the gas flowing through a strong shock is subject moderate compression, but intense heating.
. Clearly, there is a finite limit to the degree of compression of gas passing through a strong shock.
Thus, in the case of a strong shock, the large increase in the pressure across the shock front is predominately caused by a large increase in the
temperature. In other words, the gas flowing through a strong shock is subject moderate compression, but intense heating.
Finally, let us transform to a frame of reference that is co-moving with the gas upstream of the shock. In this reference frame,
the shock appears to propagate through a stationary gas of pressure, density, and temperature, 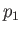 ,
, 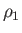 , and
, and 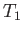 , respectively,
at the speed
, respectively,
at the speed 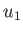 . In other words, in the new reference frame, our stationary shock is transformed into a shock wave. (See Section 14.4.)
The pressure, density, and temperature behind the wave are
. In other words, in the new reference frame, our stationary shock is transformed into a shock wave. (See Section 14.4.)
The pressure, density, and temperature behind the wave are  ,
, 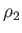 , and
, and  , respectively. Also, the
gas behind the wave follows the shock front at the speed
, respectively. Also, the
gas behind the wave follows the shock front at the speed 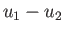 . We can regard
. We can regard
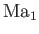 as the
Mach number of the shock wave in the unperturbed gas. It follows from Equation (14.110) that
as the
Mach number of the shock wave in the unperturbed gas. It follows from Equation (14.110) that
 |
(14.124) |
Thus, for a weak shock wave (i.e.,
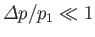 ),
),
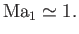 |
(14.125) |
In other words, a weak shock wave propagates through the unperturbed gas at the local sound speed. Indeed, such a
wave is essentially indistinguishable from a conventional sound wave. On the other hand, for a strong shock wave (i.e.,
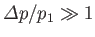 ),
),
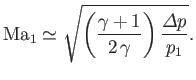 |
(14.126) |
We conclude that a strong shock wave propagates through the unperturbed gas at a speed that greatly exceeds the
local sound speed.



Next: Piston-Generated Shock Wave
Up: One-Dimensional Compressible Inviscid Flow
Previous: Sonic Flow through a
Richard Fitzpatrick
2016-03-31
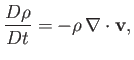
![]() . Let
. Let ![]() measure distance along the duct. The
gas's temperature,
measure distance along the duct. The
gas's temperature, ![]() , density,
, density, ![]() , pressure
, pressure ![]() , specific internal energy
, specific internal energy
![]() , and normal velocity
, and normal velocity ![]() , are all assumed to be constant across any
cross-section, and independent of time. Let the shock be situated at
, are all assumed to be constant across any
cross-section, and independent of time. Let the shock be situated at ![]() . Suppose that in the region upstream of the shock,
. Suppose that in the region upstream of the shock, ![]() , the temperature, density, pressure, specific internal energy, and
flow speed of the gas take the constant values
, the temperature, density, pressure, specific internal energy, and
flow speed of the gas take the constant values ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and ![]() , respectively. Likewise, suppose that in the region
downstream of the shock,
, respectively. Likewise, suppose that in the region
downstream of the shock, ![]() , the temperature, density, pressure, specific internal energy, and
flow speed of the gas take the constant values
, the temperature, density, pressure, specific internal energy, and
flow speed of the gas take the constant values ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and ![]() , respectively. Of course, in the immediate
vicinity of the shock,
, respectively. Of course, in the immediate
vicinity of the shock, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and ![]() are all rapidly-varying functions of
are all rapidly-varying functions of ![]() . We wish to find the
relationship between the upstream and downstream gas parameters. We can achieve this goal by invoking conservation of mass,
momentum, and energy across the shock--in other words, by making use of Equations (14.80)-(14.82).
. We wish to find the
relationship between the upstream and downstream gas parameters. We can achieve this goal by invoking conservation of mass,
momentum, and energy across the shock--in other words, by making use of Equations (14.80)-(14.82).

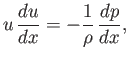
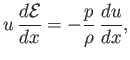
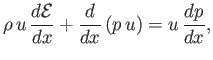
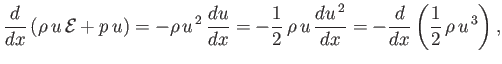
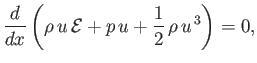


![]() ,
, ![]() , and
, and ![]() between Equations (14.100), (14.101), and
(14.103), we obtain
between Equations (14.100), (14.101), and
(14.103), we obtain

![$\displaystyle G(x) = \left(\frac{1-\gamma+2\,\gamma\,x}{\gamma+1}\right)\left[\frac{2+(\gamma-1)\,x}{(\gamma+1)\,x}\right]^{\,\gamma}.$](img5495.png)
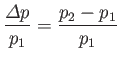
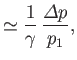
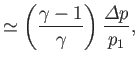
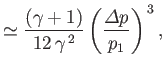
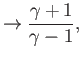

![]() ,
, ![]() , and
, and ![]() , respectively,
at the speed
, respectively,
at the speed ![]() . In other words, in the new reference frame, our stationary shock is transformed into a shock wave. (See Section 14.4.)
The pressure, density, and temperature behind the wave are
. In other words, in the new reference frame, our stationary shock is transformed into a shock wave. (See Section 14.4.)
The pressure, density, and temperature behind the wave are ![]() ,
, ![]() , and
, and ![]() , respectively. Also, the
gas behind the wave follows the shock front at the speed
, respectively. Also, the
gas behind the wave follows the shock front at the speed ![]() . We can regard
. We can regard
![]() as the
Mach number of the shock wave in the unperturbed gas. It follows from Equation (14.110) that
as the
Mach number of the shock wave in the unperturbed gas. It follows from Equation (14.110) that