


Next: Sonic Flow through a
Up: One-Dimensional Compressible Inviscid Flow
Previous: Bernoulli's Theorem
In an ideal gas, the local Mach number of the flow is
defined (see Section 1.17)
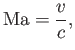 |
(14.57) |
where
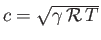 is the local sound speed. [See Equation (14.45).] Setting
is the local sound speed. [See Equation (14.45).] Setting
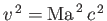 in Equation (14.55), we obtain
in Equation (14.55), we obtain
![$\displaystyle \frac{T}{T_0}=\left[1+\frac{1}{2}\,(\gamma-1)\,{\rm Ma}^{\,2}\right]^{-1},$](img5383.png) |
(14.58) |
where use has been made of Equations (14.15) and (14.24),
which imply that
Incidentally, the
relation (14.58) is valid for any streamline, because the stagnation temperature, 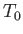 , can
be defined, by means of Equation (14.55), even when the streamline in question does not pass through a
stagnation point. We can combine Equation (14.58) with the isentropic relation,
, can
be defined, by means of Equation (14.55), even when the streamline in question does not pass through a
stagnation point. We can combine Equation (14.58) with the isentropic relation,
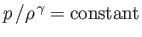 along a
streamline (see Section 14.3), as well as the ideal gas law, (14.1), to give
along a
streamline (see Section 14.3), as well as the ideal gas law, (14.1), to give
Here, 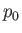 and
and 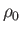 are the pressure and density, respectively, at the stagnation point.
In principle, the stagnation values,
are the pressure and density, respectively, at the stagnation point.
In principle, the stagnation values, 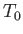 ,
, 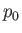 , and
, and 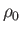 , can be different on different streamlines.
However, if a solid object moves through a homogeneous ideal gas that is asymptotically at rest then the
stagnation parameters become true constants, independent of the streamline. Such flow is said
to be homentropic.
, can be different on different streamlines.
However, if a solid object moves through a homogeneous ideal gas that is asymptotically at rest then the
stagnation parameters become true constants, independent of the streamline. Such flow is said
to be homentropic.
A point where the speed of a steadily flowing ideal gas equals the local speed of sound,  ,
is termed a sonic point. The sonic temperature,
,
is termed a sonic point. The sonic temperature, 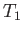 , pressure,
, pressure, 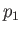 , and density,
, and density, 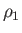 ,
are simply related to the stagnation values. In fact, setting
,
are simply related to the stagnation values. In fact, setting
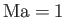 in Equations (14.58), (14.61), and (14.62), we
obtain
in Equations (14.58), (14.61), and (14.62), we
obtain
Finally, if we combine Equations (14.58), and (14.61)-(14.65), then we get



Next: Sonic Flow through a
Up: One-Dimensional Compressible Inviscid Flow
Previous: Bernoulli's Theorem
Richard Fitzpatrick
2016-03-31
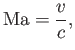
![]() ,
is termed a sonic point. The sonic temperature,
,
is termed a sonic point. The sonic temperature, ![]() , pressure,
, pressure, ![]() , and density,
, and density, ![]() ,
are simply related to the stagnation values. In fact, setting
,
are simply related to the stagnation values. In fact, setting
![]() in Equations (14.58), (14.61), and (14.62), we
obtain
in Equations (14.58), (14.61), and (14.62), we
obtain