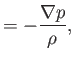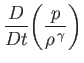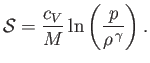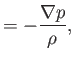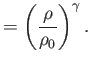Next: Fluid Equations in Cartesian
Up: Mathematical Models of Fluid
Previous: Dimensionless Numbers in Incompressible
Dimensionless Numbers in Compressible Flow
It is helpful to normalize the equations of compressible ideal gas flow, (1.87)-(1.89), in the following
manner:
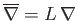 ,
,
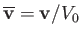 ,
,
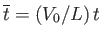 ,
,
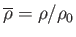 ,
,
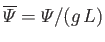 ,
,
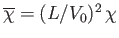 , and
, and
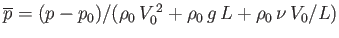 . Here,
. Here, 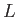 is a typical spatial variation lengthscale,
is a typical spatial variation lengthscale, 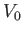 a typical fluid velocity,
a typical fluid velocity, 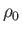 a typical mass density, and
a typical mass density, and 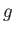 a typical gravitational acceleration (assuming that
a typical gravitational acceleration (assuming that
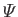 represents a gravitational
potential energy per unit mass). Furthermore,
represents a gravitational
potential energy per unit mass). Furthermore, 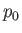 corresponds to atmospheric pressure at ground level, and is a uniform
constant. It follows that
corresponds to atmospheric pressure at ground level, and is a uniform
constant. It follows that
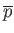 represents deviations from atmospheric pressure.
All barred quantities are dimensionless, and are designed to be comparable with unity.
The normalized equations of compressible ideal gas flow take the form
represents deviations from atmospheric pressure.
All barred quantities are dimensionless, and are designed to be comparable with unity.
The normalized equations of compressible ideal gas flow take the form
where
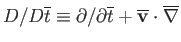 ,
,
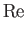 |
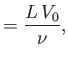 |
(1.106) |
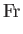 |
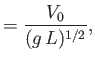 |
(1.107) |
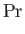 |
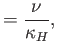 |
(1.108) |
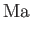 |
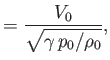 |
(1.109) |
and
Here, the dimensionless numbers 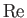 ,
, 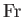 ,
, 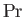 , and
, and 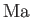 are known as the Reynolds number,
Froude number, Prandtl number, and Mach number, respectively. [The latter two
numbers are named after Ludwig Prandtl (1875-1953) and Ernst Mach (1838-1916), respectively.] The Reynolds number is the typical ratio of inertial to viscous forces within the gas,
the square of the Froude number is the typical ratio of inertial to gravitational forces, the Prandtl number
is the typical ratio of the momentum and thermal diffusion rates,
and the Mach number is the typical ratio of the
gas flow and sound propagation speeds. Thus, thermal diffusion is far faster than momentum diffusion when
are known as the Reynolds number,
Froude number, Prandtl number, and Mach number, respectively. [The latter two
numbers are named after Ludwig Prandtl (1875-1953) and Ernst Mach (1838-1916), respectively.] The Reynolds number is the typical ratio of inertial to viscous forces within the gas,
the square of the Froude number is the typical ratio of inertial to gravitational forces, the Prandtl number
is the typical ratio of the momentum and thermal diffusion rates,
and the Mach number is the typical ratio of the
gas flow and sound propagation speeds. Thus, thermal diffusion is far faster than momentum diffusion when
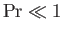 ,
and vice versa. Moreover, the gas flow is termed subsonic when
,
and vice versa. Moreover, the gas flow is termed subsonic when
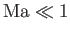 , supersonic when
, supersonic when
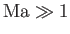 , and transonic when
, and transonic when
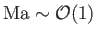 .
Note that
.
Note that
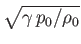 is the speed of sound in the undisturbed gas (Reif 1965).
The quantity
is the speed of sound in the undisturbed gas (Reif 1965).
The quantity 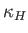 is called the thermal diffusivity of the gas, and has
units of meters squared per second. Thus, heat typically diffuses through the gas a distance
is called the thermal diffusivity of the gas, and has
units of meters squared per second. Thus, heat typically diffuses through the gas a distance
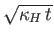 meters in
meters in 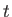 seconds.
The thermal diffusivity of dry air at atmospheric
pressure and
seconds.
The thermal diffusivity of dry air at atmospheric
pressure and
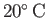 is about
is about
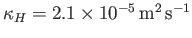 (Batchelor 2000).
It follows that heat diffusion in air is a relatively slow process.
The kinematic viscosity of dry air at atmospheric pressure and
(Batchelor 2000).
It follows that heat diffusion in air is a relatively slow process.
The kinematic viscosity of dry air at atmospheric pressure and
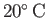 is
about
is
about
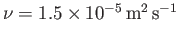 (Batchelor 2000). Hence, momentum diffusion in air
is also a relatively slow process.
(Batchelor 2000). Hence, momentum diffusion in air
is also a relatively slow process.
For the case of dry air at atmospheric pressure and
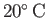 (Batchelor 2000),
(Batchelor 2000),
Thus, if
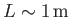 and
and
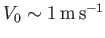 , as is often the case for subsonic
air dynamics close to the Earth's surface, then the previous expressions suggest that
, as is often the case for subsonic
air dynamics close to the Earth's surface, then the previous expressions suggest that
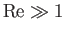 ,
,
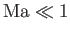 , and
, and
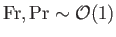 . It immediately follows from Equation (1.105) that
. It immediately follows from Equation (1.105) that
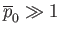 .
However, in this situation, Equation (1.104) is dominated by the second term in square brackets on
its left-hand side. Hence, this equation can only be satisfied if the term in question is small, which implies that
.
However, in this situation, Equation (1.104) is dominated by the second term in square brackets on
its left-hand side. Hence, this equation can only be satisfied if the term in question is small, which implies that
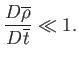 |
(1.116) |
Equation (1.102) then gives
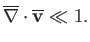 |
(1.117) |
It is evident that subsonic (i.e.,
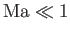 ) gas flow is essentially incompressible.
The fact that
) gas flow is essentially incompressible.
The fact that
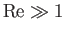 implies that such flow is also essentially inviscid. In the
incompressible inviscid limit (in which
implies that such flow is also essentially inviscid. In the
incompressible inviscid limit (in which
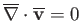 and
and
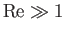 ), the
(unnormalized) compressible ideal gas flow equations
reduce to the previously derived, inviscid, incompressible, fluid flow equations:
), the
(unnormalized) compressible ideal gas flow equations
reduce to the previously derived, inviscid, incompressible, fluid flow equations:
It follows that the equations which govern subsonic gas dynamics close to the surface of the Earth are essentially the
same as those that govern the flow of water.
Suppose that
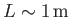 and
and
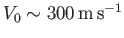 , as is typically the case for transonic
air dynamics (e.g., air flow over the wing of a fighter jet). In this situation,
Equations (1.105) and (1.112)-(1.115) yield
, as is typically the case for transonic
air dynamics (e.g., air flow over the wing of a fighter jet). In this situation,
Equations (1.105) and (1.112)-(1.115) yield
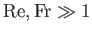 and
and
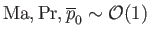 . It follows that the final two terms on the right-hand sides of Equations (1.103) and
(1.104) can be neglected. Thus, the (unnormalized) compressible ideal gas flow equations reduce to the
following set of inviscid, adiabatic, ideal gas, flow equations:
. It follows that the final two terms on the right-hand sides of Equations (1.103) and
(1.104) can be neglected. Thus, the (unnormalized) compressible ideal gas flow equations reduce to the
following set of inviscid, adiabatic, ideal gas, flow equations:
In particular, if the initial distribution of
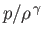 is uniform in space, as is often the case, then Equation (1.122) ensures that the distribution remains uniform as time progresses. In fact, it can be shown that the entropy
per unit mass of an ideal gas is (Reif 1965)
is uniform in space, as is often the case, then Equation (1.122) ensures that the distribution remains uniform as time progresses. In fact, it can be shown that the entropy
per unit mass of an ideal gas is (Reif 1965)
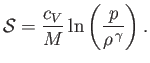 |
(1.123) |
Hence, the assumption that
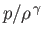 is uniform in space is equivalent to the assumption that the
entropy per unit mass of the gas is a spatial constant. A gas for which this is the case is termed homentropic.
Equation (1.122) ensures that the entropy of a co-moving gas element is a constant of the motion in
transonic flow. A gas for which this is the case is termed isentropic.
In the homentropic case, the previous compressible gas flow equations simplify
somewhat to give
is uniform in space is equivalent to the assumption that the
entropy per unit mass of the gas is a spatial constant. A gas for which this is the case is termed homentropic.
Equation (1.122) ensures that the entropy of a co-moving gas element is a constant of the motion in
transonic flow. A gas for which this is the case is termed isentropic.
In the homentropic case, the previous compressible gas flow equations simplify
somewhat to give
Here, 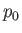 is atmospheric pressure, and
is atmospheric pressure, and 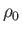 is the density of air at atmospheric pressure. Equation (1.126)
is known as the adiabatic gas law, and is a consequence of the fact that transonic gas dynamics takes place
far too quickly for thermal heat conduction (which is a relatively slow process) to have any appreciable effect on the temperature distribution within the gas. Incidentally, a gas in which thermal diffusion is negligible is generally termed adiabatic.
is the density of air at atmospheric pressure. Equation (1.126)
is known as the adiabatic gas law, and is a consequence of the fact that transonic gas dynamics takes place
far too quickly for thermal heat conduction (which is a relatively slow process) to have any appreciable effect on the temperature distribution within the gas. Incidentally, a gas in which thermal diffusion is negligible is generally termed adiabatic.



Next: Fluid Equations in Cartesian
Up: Mathematical Models of Fluid
Previous: Dimensionless Numbers in Incompressible
Richard Fitzpatrick
2016-03-31
![$\displaystyle = - \left(1+\frac{1}{{\rm Fr}^{\,2}}+\frac{1}{{\rm Re}}\right)\fr...
...-\frac{1}{3}\,\overline{\nabla}(\overline{\nabla}\cdot\overline{\bf v})\right],$](img395.png)
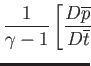
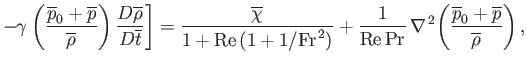
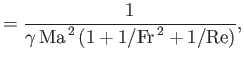
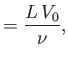
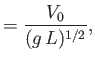
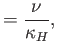
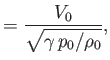
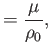
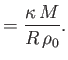
![]() (Batchelor 2000),
(Batchelor 2000),
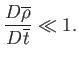
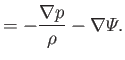
![]() and
and
![]() , as is typically the case for transonic
air dynamics (e.g., air flow over the wing of a fighter jet). In this situation,
Equations (1.105) and (1.112)-(1.115) yield
, as is typically the case for transonic
air dynamics (e.g., air flow over the wing of a fighter jet). In this situation,
Equations (1.105) and (1.112)-(1.115) yield
![]() and
and
![]() . It follows that the final two terms on the right-hand sides of Equations (1.103) and
(1.104) can be neglected. Thus, the (unnormalized) compressible ideal gas flow equations reduce to the
following set of inviscid, adiabatic, ideal gas, flow equations:
. It follows that the final two terms on the right-hand sides of Equations (1.103) and
(1.104) can be neglected. Thus, the (unnormalized) compressible ideal gas flow equations reduce to the
following set of inviscid, adiabatic, ideal gas, flow equations: