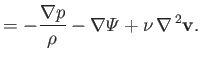Next: Dimensionless Numbers in Compressible
Up: Mathematical Models of Fluid
Previous: Equations of Compressible Fluid
Dimensionless Numbers in Incompressible Flow
It is helpful to normalize the equations of incompressible fluid flow, (1.81)-(1.82), in the following
manner:
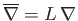 ,
,
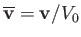 ,
,
 ,
,
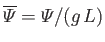 , and
, and
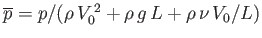 . Here,
. Here,  is a typical spatial variation lengthscale,
is a typical spatial variation lengthscale, 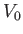 a typical fluid velocity, and
a typical fluid velocity, and 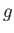 a typical gravitational acceleration (assuming that
a typical gravitational acceleration (assuming that
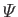 represents a gravitational
potential energy per unit mass). All barred quantities are dimensionless, and are designed to be comparable with unity.
The normalized equations of incompressible fluid flow take the form
represents a gravitational
potential energy per unit mass). All barred quantities are dimensionless, and are designed to be comparable with unity.
The normalized equations of incompressible fluid flow take the form
where
 , and
, and
Here, the dimensionless quantities 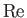 and
and 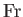 are known as the Reynolds number and the
Froude number, respectively. [After Osborne Reynolds (1842-1912) and William Froude (1810-1879), respectively.] The Reynolds number is the typical ratio of inertial to viscous forces within the fluid,
whereas the square of the Froude number is the typical ratio of inertial to gravitational forces. Thus, viscosity is relatively important
compared to inertia when
are known as the Reynolds number and the
Froude number, respectively. [After Osborne Reynolds (1842-1912) and William Froude (1810-1879), respectively.] The Reynolds number is the typical ratio of inertial to viscous forces within the fluid,
whereas the square of the Froude number is the typical ratio of inertial to gravitational forces. Thus, viscosity is relatively important
compared to inertia when
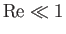 , and vice versa. Likewise, gravity is relatively important compared to
inertia when
, and vice versa. Likewise, gravity is relatively important compared to
inertia when
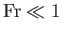 , and
vice versa.
Note that, in principal,
, and
vice versa.
Note that, in principal, 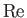 and
and 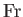 are the only quantities in Equations (1.90) and (1.91) that can be significantly greater or smaller
than unity.
are the only quantities in Equations (1.90) and (1.91) that can be significantly greater or smaller
than unity.
For the case of water at
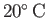 , located on the surface of the Earth (Batchelor 2000),
, located on the surface of the Earth (Batchelor 2000),
Thus, if
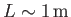 and
and
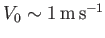 , as is often the
case for terrestrial water dynamics, then the previous expressions suggest that
, as is often the
case for terrestrial water dynamics, then the previous expressions suggest that
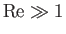 and
and
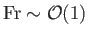 .
In this situation, the viscous term on the right-hand side of Equation (1.91) becomes negligible,
and the (unnormalized) incompressible fluid flow equations
reduce to the following inviscid, incompressible, fluid flow equations:
.
In this situation, the viscous term on the right-hand side of Equation (1.91) becomes negligible,
and the (unnormalized) incompressible fluid flow equations
reduce to the following inviscid, incompressible, fluid flow equations:
For the case of lubrication oil at
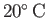 , located on the surface of the Earth,
, located on the surface of the Earth,
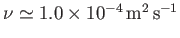 (i.e.,
oil is about 100 times more viscous than water), and
so (Batchelor 2000)
(i.e.,
oil is about 100 times more viscous than water), and
so (Batchelor 2000)
Suppose that oil is slowly flowing down a narrow lubrication channel such that
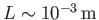 and
and
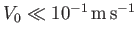 .
It follows, from the previous expressions, that
.
It follows, from the previous expressions, that
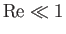 and
and
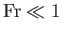 . In this situation, the inertial term on the left-hand
side of (1.91) becomes negligible, and the (unnormalized)
incompressible fluid flow equations
reduce to the following inertia-free, incompressible, fluid flow equations:
. In this situation, the inertial term on the left-hand
side of (1.91) becomes negligible, and the (unnormalized)
incompressible fluid flow equations
reduce to the following inertia-free, incompressible, fluid flow equations:



Next: Dimensionless Numbers in Compressible
Up: Mathematical Models of Fluid
Previous: Equations of Compressible Fluid
Richard Fitzpatrick
2016-03-31
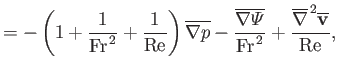
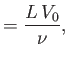
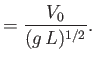
![]() , located on the surface of the Earth (Batchelor 2000),
, located on the surface of the Earth (Batchelor 2000),
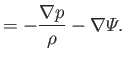
![]() , located on the surface of the Earth,
, located on the surface of the Earth,
![]() (i.e.,
oil is about 100 times more viscous than water), and
so (Batchelor 2000)
(i.e.,
oil is about 100 times more viscous than water), and
so (Batchelor 2000)