Next: Equations of Compressible Fluid
Up: Mathematical Models of Fluid
Previous: Energy Conservation
Equations of Incompressible Fluid Flow
In most situations of general interest, the flow of a conventional liquid, such as water, is incompressible to
a high degree of accuracy. A fluid is said to be incompressible when the mass density of a co-moving volume element
does not change appreciably as the element moves through regions of varying pressure. In other words, for an incompressible fluid, the rate of change of 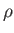 following the motion is zero: that is,
following the motion is zero: that is,
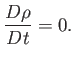 |
(1.76) |
In this case, the continuity equation (1.40) reduces to
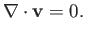 |
(1.77) |
We conclude that, as a consequence of mass conservation, an incompressible fluid must have a divergence-free, or solenoidal, velocity field. This immediately implies, from Equation (1.42), that the volume of a co-moving fluid element is a constant of the motion. In most practical situations, the initial density distribution in an incompressible fluid is uniform in space.
Hence, it follows from Equation (1.76) that the density distribution remains uniform in space and constant in time.
In other words, we can generally treat the density, 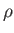 , as a uniform constant in incompressible fluid flow problems.
, as a uniform constant in incompressible fluid flow problems.
Suppose that the volume force acting on the fluid is conservative in nature (see Section A.18): that is,
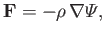 |
(1.78) |
where
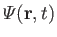 is the potential energy per unit mass, and
is the potential energy per unit mass, and
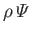 the
potential energy per unit volume. Assuming that the fluid viscosity is a spatially uniform quantity, which is
generally the case (unless there are strong temperature variations within the fluid), the Navier-Stokes equation for an incompressible fluid reduces to
the
potential energy per unit volume. Assuming that the fluid viscosity is a spatially uniform quantity, which is
generally the case (unless there are strong temperature variations within the fluid), the Navier-Stokes equation for an incompressible fluid reduces to
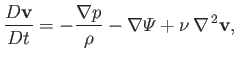 |
(1.79) |
where
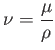 |
(1.80) |
is termed the kinematic viscosity, and has units of meters squared per second.
Roughly speaking, momentum diffuses a distance of order
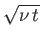 meters in
meters in 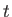 seconds as a consequence of viscosity.
The kinematic viscosity of water at
seconds as a consequence of viscosity.
The kinematic viscosity of water at
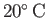 is about
is about
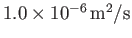 (Batchelor 2000).
It follows that viscous momentum diffusion in water is a relatively slow process.
(Batchelor 2000).
It follows that viscous momentum diffusion in water is a relatively slow process.
The complete set of equations governing incompressible flow is
Here, 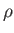 and
and 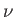 are regarded as known constants, and
are regarded as known constants, and
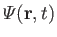 as a known function. Thus, we have
four equations--namely, Equation (1.81), plus the three components of Equation (1.82)--for
four unknowns--namely, the pressure,
as a known function. Thus, we have
four equations--namely, Equation (1.81), plus the three components of Equation (1.82)--for
four unknowns--namely, the pressure,
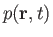 , plus the three components of the velocity,
, plus the three components of the velocity,
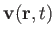 .
Note that an energy conservation equation is redundant in the case of incompressible fluid flow.
.
Note that an energy conservation equation is redundant in the case of incompressible fluid flow.



Next: Equations of Compressible Fluid
Up: Mathematical Models of Fluid
Previous: Energy Conservation
Richard Fitzpatrick
2016-03-31