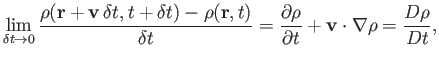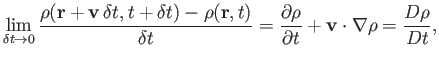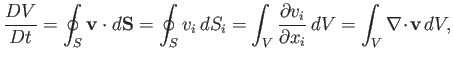Next: Momentum Conservation
Up: Mathematical Models of Fluid
Previous: Mass Conservation
Convective Time Derivative
The quantity
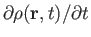 , appearing in Equation (1.37), represents the time derivative of the fluid mass density at the fixed point
, appearing in Equation (1.37), represents the time derivative of the fluid mass density at the fixed point  . Suppose that
. Suppose that
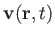 is the instantaneous fluid velocity at the same point. It follows
that the time derivative of the density, as seen in a frame of reference which is instantaneously co-moving with the fluid
at point
is the instantaneous fluid velocity at the same point. It follows
that the time derivative of the density, as seen in a frame of reference which is instantaneously co-moving with the fluid
at point  , is
, is
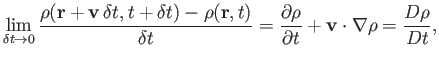 |
(1.38) |
where we have Taylor expanded
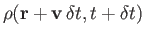 up to first order in
up to first order in 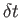 , and where
, and where
 |
(1.39) |
Clearly, the so-called convective time derivative,  , represents the time derivative seen in the local rest frame of the fluid.
, represents the time derivative seen in the local rest frame of the fluid.
The continuity equation (1.37) can be rewritten in the form
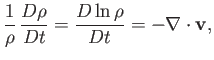 |
(1.40) |
because
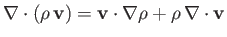 . [See Equation (A.174).] Consider a
volume element
. [See Equation (A.174).] Consider a
volume element  that is co-moving with the fluid.
In general, as the element is convected by the fluid its volume changes. In fact, it is easily
seen that
that is co-moving with the fluid.
In general, as the element is convected by the fluid its volume changes. In fact, it is easily
seen that
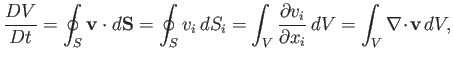 |
(1.41) |
where  is the bounding surface of the element, and use has been made of the divergence theorem. In the limit that
is the bounding surface of the element, and use has been made of the divergence theorem. In the limit that
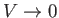 ,
and
,
and
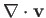 is approximately constant across the element, we obtain
is approximately constant across the element, we obtain
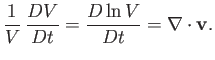 |
(1.42) |
Hence, we conclude that the divergence of the fluid velocity at a given point in space specifies
the fractional rate of increase in the volume of an infinitesimal co-moving fluid element at that point.



Next: Momentum Conservation
Up: Mathematical Models of Fluid
Previous: Mass Conservation
Richard Fitzpatrick
2016-03-31