


Next: Fluid Equations in Cylindrical
Up: Mathematical Models of Fluid
Previous: Dimensionless Numbers in Compressible
Fluid Equations in Cartesian Coordinates
Let us adopt the conventional Cartesian coordinate system, ( ,
,  ,
,  ). According to Equation (1.26), the various components
of the stress tensor are
). According to Equation (1.26), the various components
of the stress tensor are
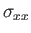 |
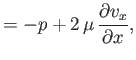 |
(1.127) |
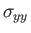 |
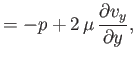 |
(1.128) |
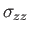 |
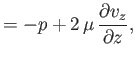 |
(1.129) |
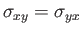 |
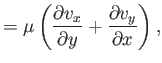 |
(1.130) |
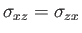 |
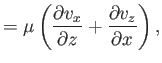 |
(1.131) |
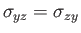 |
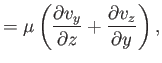 |
(1.132) |
where 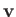 is the velocity,
is the velocity, 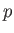 the pressure, and
the pressure, and 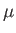 the viscosity. The equations of compressible
fluid flow, (1.87)-(1.89) (from which the equations of incompressible fluid flow
can easily be obtained by setting
the viscosity. The equations of compressible
fluid flow, (1.87)-(1.89) (from which the equations of incompressible fluid flow
can easily be obtained by setting
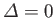 ), become
), become
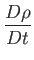 |
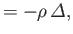 |
(1.133) |
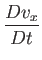 |
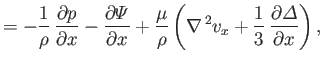 |
(1.134) |
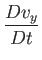 |
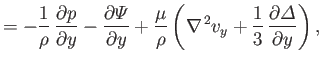 |
(1.135) |
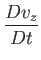 |
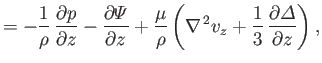 |
(1.136) |
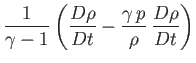 |
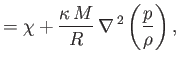 |
(1.137) |
where 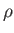 is the mass density,
is the mass density, 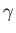 the ratio of specific heats,
the ratio of specific heats, 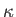 the heat conductivity,
the heat conductivity, 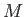 the molar mass, and
the molar mass, and 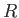 the molar ideal gas constant. Furthermore,
the molar ideal gas constant. Furthermore,
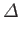 |
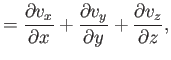 |
(1.138) |
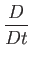 |
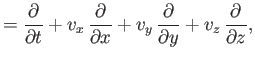 |
(1.139) |
 |
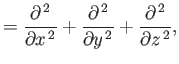 |
(1.140) |
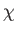 |
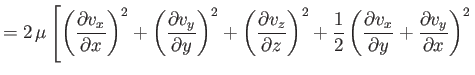 |
|
| |
![$\displaystyle \phantom{=}\left.+\frac{1}{2}\left(\frac{\partial v_x}{\partial z...
...frac{\partial v_y}{\partial z}+\frac{\partial v_z}{\partial y}\right)^2\right].$](img471.png) |
(1.141) |
Here, 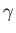 ,
, 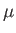 ,
, 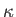 , and
, and 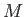 are treated as uniform constants.
are treated as uniform constants.



Next: Fluid Equations in Cylindrical
Up: Mathematical Models of Fluid
Previous: Dimensionless Numbers in Compressible
Richard Fitzpatrick
2016-03-31
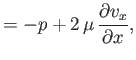
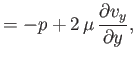
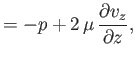
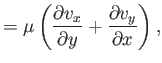
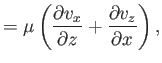
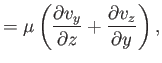
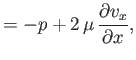
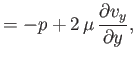
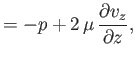
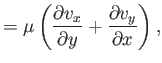
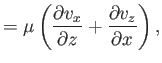
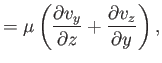
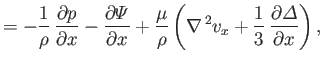
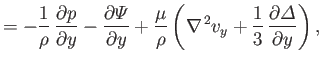
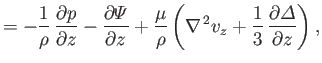
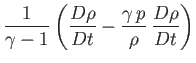
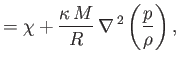
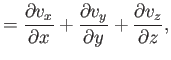
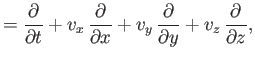
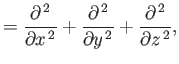
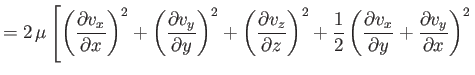
![$\displaystyle \phantom{=}\left.+\frac{1}{2}\left(\frac{\partial v_x}{\partial z...
...frac{\partial v_y}{\partial z}+\frac{\partial v_z}{\partial y}\right)^2\right].$](img471.png)