

Next: Fluid Equations in Spherical
Up: Mathematical Models of Fluid
Previous: Fluid Equations in Cartesian
Fluid Equations in Cylindrical Coordinates
Let us adopt the cylindrical coordinate system, (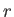 ,
, 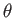 ,
, 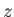 ). Making use of the results quoted
in Section C.3, the components of the stress tensor are
). Making use of the results quoted
in Section C.3, the components of the stress tensor are
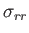 |
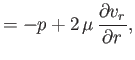 |
(1.142) |
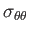 |
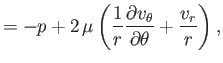 |
(1.143) |
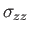 |
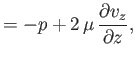 |
(1.144) |
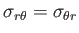 |
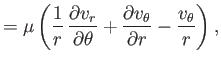 |
(1.145) |
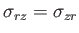 |
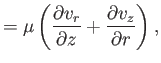 |
(1.146) |
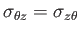 |
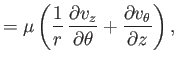 |
(1.147) |
whereas the equations of compressible fluid flow become
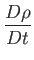 |
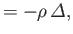 |
(1.148) |
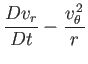 |
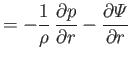 |
|
| |
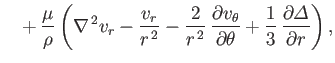 |
(1.149) |
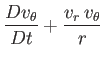 |
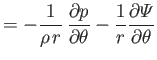 |
|
| |
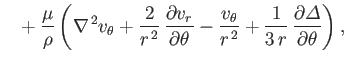 |
(1.150) |
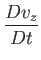 |
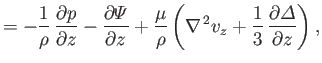 |
(1.151) |
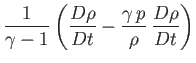 |
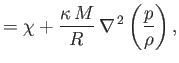 |
(1.152) |
where


Next: Fluid Equations in Spherical
Up: Mathematical Models of Fluid
Previous: Fluid Equations in Cartesian
Richard Fitzpatrick
2016-03-31
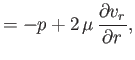
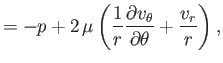
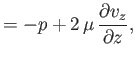
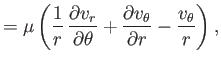
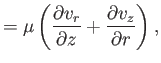
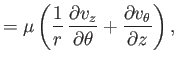
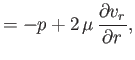
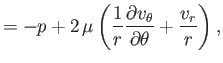
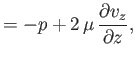
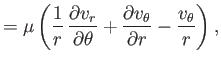
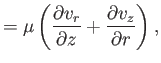
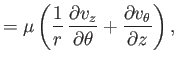
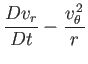
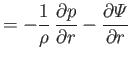
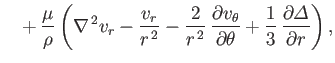
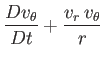
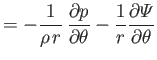
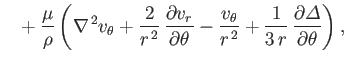
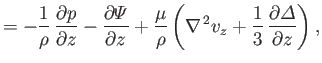
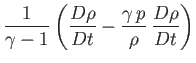
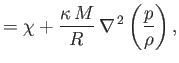
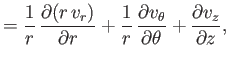
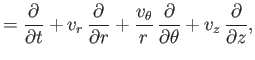
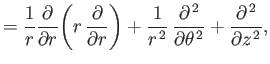
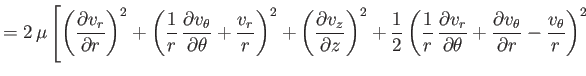
![$\displaystyle \phantom{=}\left.+\frac{1}{2}\left(\frac{\partial v_r}{\partial z...
...{\partial z}+\frac{1}{r}\,\frac{\partial v_z}{\partial \theta}\right)^2\right].$](img494.png)