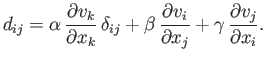Next: Viscosity
Up: Mathematical Models of Fluid
Previous: Stress Tensor in a
Stress Tensor in a Moving Fluid
We have seen that in a static fluid the stress tensor takes the form
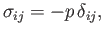 |
(1.15) |
where
 is the static pressure: that is, minus the normal stress acting in any direction.
The normal stress at a given point in a moving fluid generally varies with direction. In other words, the principal stresses are
not equal to one another. However, we can still define the mean principal stress as
is the static pressure: that is, minus the normal stress acting in any direction.
The normal stress at a given point in a moving fluid generally varies with direction. In other words, the principal stresses are
not equal to one another. However, we can still define the mean principal stress as
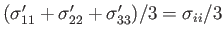 .
Moreover, given that the principal stresses are actually normal stresses (in a coordinate frame aligned with the principal axes), we can also regard
.
Moreover, given that the principal stresses are actually normal stresses (in a coordinate frame aligned with the principal axes), we can also regard
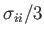 as the mean normal stress.
It is convenient to define pressure in a moving fluid as minus the mean normal
stress: that is,
as the mean normal stress.
It is convenient to define pressure in a moving fluid as minus the mean normal
stress: that is,
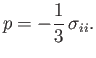 |
(1.16) |
Thus, we can write the stress tensor in a moving fluid as the sum of an isotropic part,
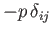 ,
which has the same form as the stress tensor in a static fluid, and a remaining non-isotropic
part,
,
which has the same form as the stress tensor in a static fluid, and a remaining non-isotropic
part, 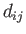 , which includes any shear stresses, and also has diagonal components whose
sum is zero. In other words,
, which includes any shear stresses, and also has diagonal components whose
sum is zero. In other words,
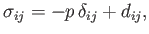 |
(1.17) |
where
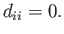 |
(1.18) |
Moreover, because
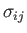 and
and
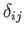 are both symmetric tensors, it follows that
are both symmetric tensors, it follows that
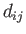 is also symmetric: that is,
is also symmetric: that is,
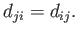 |
(1.19) |
It is clear that the so-called deviatoric stress tensor, 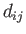 , is a consequence of fluid motion, because
it is zero in a static fluid. Suppose, however, that we were to view a static fluid both in its rest frame and in a frame of reference moving at
some constant velocity relative to the rest frame. We would expect the force distribution within the fluid to
be the same in both frames of reference, because the fluid does not accelerate in either.
However, in the first frame, the fluid appears stationary and the deviatoric stress tensor is therefore zero, while in the second it has a spatially uniform velocity field and the deviatoric stress tensor is also zero (because it is the same as in the rest frame).
We, thus, conclude that the deviatoric stress tensor is zero both in a stationary fluid and in a moving fluid
possessing no spatial velocity gradients. This suggests that the deviatoric stress tensor is driven by velocity gradients
within the fluid. Moreover, the tensor must vanish as these gradients vanish.
, is a consequence of fluid motion, because
it is zero in a static fluid. Suppose, however, that we were to view a static fluid both in its rest frame and in a frame of reference moving at
some constant velocity relative to the rest frame. We would expect the force distribution within the fluid to
be the same in both frames of reference, because the fluid does not accelerate in either.
However, in the first frame, the fluid appears stationary and the deviatoric stress tensor is therefore zero, while in the second it has a spatially uniform velocity field and the deviatoric stress tensor is also zero (because it is the same as in the rest frame).
We, thus, conclude that the deviatoric stress tensor is zero both in a stationary fluid and in a moving fluid
possessing no spatial velocity gradients. This suggests that the deviatoric stress tensor is driven by velocity gradients
within the fluid. Moreover, the tensor must vanish as these gradients vanish.
Let the
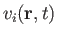 be the Cartesian components of the fluid velocity at point
be the Cartesian components of the fluid velocity at point  and time
and time 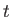 . The
various velocity gradients within the fluid then take the form
. The
various velocity gradients within the fluid then take the form
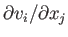 . The simplest
possible assumption, which is consistent with the previous discussion, is that the components of the deviatoric stress tensor are linear functions
of these velocity gradients: that is,
. The simplest
possible assumption, which is consistent with the previous discussion, is that the components of the deviatoric stress tensor are linear functions
of these velocity gradients: that is,
 |
(1.20) |
Here, 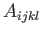 is a fourth-order tensor (this follows from the quotient rule because
is a fourth-order tensor (this follows from the quotient rule because 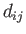 and
and
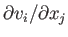 are both proper second-order tensors). Any fluid in which the deviatoric
stress tensor takes the previous form is termed a Newtonian fluid, because Newton was the
first to postulate a linear relationship between shear stresses and velocity gradients.
are both proper second-order tensors). Any fluid in which the deviatoric
stress tensor takes the previous form is termed a Newtonian fluid, because Newton was the
first to postulate a linear relationship between shear stresses and velocity gradients.
In an isotropic fluid--that is, a fluid in which there is no preferred direction--we would
expect the fourth-order tensor 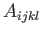 to be isotropic--that is, to have a form in which all physical
distinction between different directions is absent. As demonstrated in Section B.5, the
most general expression for an isotropic fourth-order tensor is
to be isotropic--that is, to have a form in which all physical
distinction between different directions is absent. As demonstrated in Section B.5, the
most general expression for an isotropic fourth-order tensor is
 |
(1.21) |
where  ,
, 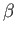 , and
, and 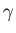 are arbitrary scalars (which can be functions of position and time).
Thus, it follows from Equations (1.20) and (1.21) that
are arbitrary scalars (which can be functions of position and time).
Thus, it follows from Equations (1.20) and (1.21) that
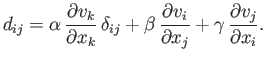 |
(1.22) |
However, according to Equation (1.19), 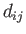 is a symmetric tensor, which implies that
is a symmetric tensor, which implies that
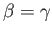 ,
and
,
and
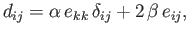 |
(1.23) |
where
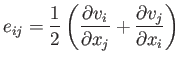 |
(1.24) |
is called the rate of strain tensor.
Finally, according to Equation (1.18), 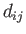 is a traceless tensor, which yields
is a traceless tensor, which yields
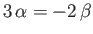 , and
, and
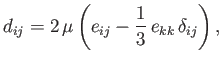 |
(1.25) |
where 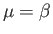 .
We, thus, conclude that the most general expression for the stress tensor in an isotropic Newtonian fluid
is
.
We, thus, conclude that the most general expression for the stress tensor in an isotropic Newtonian fluid
is
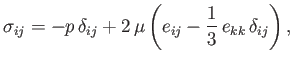 |
(1.26) |
where
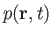 and
and
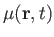 are arbitrary scalars.
are arbitrary scalars.



Next: Viscosity
Up: Mathematical Models of Fluid
Previous: Stress Tensor in a
Richard Fitzpatrick
2016-03-31
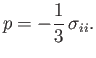
![]() , is a consequence of fluid motion, because
it is zero in a static fluid. Suppose, however, that we were to view a static fluid both in its rest frame and in a frame of reference moving at
some constant velocity relative to the rest frame. We would expect the force distribution within the fluid to
be the same in both frames of reference, because the fluid does not accelerate in either.
However, in the first frame, the fluid appears stationary and the deviatoric stress tensor is therefore zero, while in the second it has a spatially uniform velocity field and the deviatoric stress tensor is also zero (because it is the same as in the rest frame).
We, thus, conclude that the deviatoric stress tensor is zero both in a stationary fluid and in a moving fluid
possessing no spatial velocity gradients. This suggests that the deviatoric stress tensor is driven by velocity gradients
within the fluid. Moreover, the tensor must vanish as these gradients vanish.
, is a consequence of fluid motion, because
it is zero in a static fluid. Suppose, however, that we were to view a static fluid both in its rest frame and in a frame of reference moving at
some constant velocity relative to the rest frame. We would expect the force distribution within the fluid to
be the same in both frames of reference, because the fluid does not accelerate in either.
However, in the first frame, the fluid appears stationary and the deviatoric stress tensor is therefore zero, while in the second it has a spatially uniform velocity field and the deviatoric stress tensor is also zero (because it is the same as in the rest frame).
We, thus, conclude that the deviatoric stress tensor is zero both in a stationary fluid and in a moving fluid
possessing no spatial velocity gradients. This suggests that the deviatoric stress tensor is driven by velocity gradients
within the fluid. Moreover, the tensor must vanish as these gradients vanish.
![]() be the Cartesian components of the fluid velocity at point
be the Cartesian components of the fluid velocity at point ![]() and time
and time ![]() . The
various velocity gradients within the fluid then take the form
. The
various velocity gradients within the fluid then take the form
![]() . The simplest
possible assumption, which is consistent with the previous discussion, is that the components of the deviatoric stress tensor are linear functions
of these velocity gradients: that is,
. The simplest
possible assumption, which is consistent with the previous discussion, is that the components of the deviatoric stress tensor are linear functions
of these velocity gradients: that is,
![]() to be isotropic--that is, to have a form in which all physical
distinction between different directions is absent. As demonstrated in Section B.5, the
most general expression for an isotropic fourth-order tensor is
to be isotropic--that is, to have a form in which all physical
distinction between different directions is absent. As demonstrated in Section B.5, the
most general expression for an isotropic fourth-order tensor is