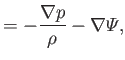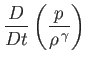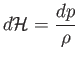Next: Sound Waves
Up: One-Dimensional Compressible Inviscid Flow
Previous: Thermodynamic Considerations
Isentropic Flow
In the limit of vanishing viscosity and heat conduction, the equations of compressible
ideal gas flow, introduced in Section 1.15, can be written
where 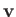 is the flow velocity, and
is the flow velocity, and
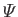 the potential energy per unit mass.
It is clear from Equations (14.25) and (14.32) that the specific entropy is constant along a streamline, but not necessarily the
same constant on different streamlines.
Such flow is said to be isentropic. From Equation (14.29), isentropic flow is characterized by
the potential energy per unit mass.
It is clear from Equations (14.25) and (14.32) that the specific entropy is constant along a streamline, but not necessarily the
same constant on different streamlines.
Such flow is said to be isentropic. From Equation (14.29), isentropic flow is characterized by
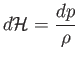 |
(14.33) |
along a streamline.
More generally, isentropic flow is characterized by
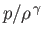 ,
,
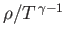 , and
, and
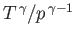 ,
constant along streamlines.
,
constant along streamlines.
Richard Fitzpatrick
2016-03-31