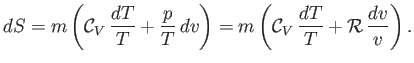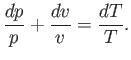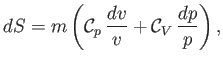Next: Isentropic Flow
Up: One-Dimensional Compressible Inviscid Flow
Previous: Introduction
Thermodynamic Considerations
Consider a quantity of gas contained in some form of enclosure. If the system is left alone
for a sufficiently long time then it will attain an equilibrium state in which all
macroscopically measurable quantities become independent of time. Examples of
such quantities are the mass, 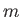 , the pressure,
, the pressure, 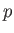 , the volume,
, the volume, 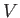 , and the absolute
temperature,
, and the absolute
temperature, 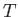 . It is helpful to distinguish between so-called extensive and
intensive equilibrium quantities. A quantity is said to be extensive if it is proportional to the mass of the gas present in the enclosure.
On the other hand, a quantity is said to be intensive if it is independent of the mass.
Thus, the mass,
. It is helpful to distinguish between so-called extensive and
intensive equilibrium quantities. A quantity is said to be extensive if it is proportional to the mass of the gas present in the enclosure.
On the other hand, a quantity is said to be intensive if it is independent of the mass.
Thus, the mass, 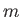 , and volume,
, and volume, 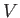 , are extensive quantities, whereas the pressure,
, are extensive quantities, whereas the pressure, 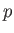 , and
the absolute temperature,
, and
the absolute temperature, 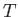 , are intensive. For every extensive quantity (except the mass), we can
introduce a corresponding intensive quantity by dividing by the mass. For instance, the
intensive quantity that corresponds to the volume,
, are intensive. For every extensive quantity (except the mass), we can
introduce a corresponding intensive quantity by dividing by the mass. For instance, the
intensive quantity that corresponds to the volume, 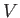 , is the specific volume,
, is the specific volume, 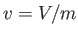 ,
which is simply the volume per unit mass (i.e., the volume of a unit mass of gas).
Of course,
,
which is simply the volume per unit mass (i.e., the volume of a unit mass of gas).
Of course, 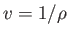 , where
, where 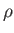 is the mass density.
is the mass density.
A gas is said to be ideal if it obeys the law (Reif 1965),
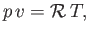 |
(14.1) |
where the constant 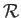 is termed the specific gas constant. This quantity is related to the
molar gas constant,
is termed the specific gas constant. This quantity is related to the
molar gas constant, 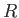 , introduced in Section 1.15, according to
, introduced in Section 1.15, according to
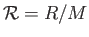 , where
, where 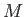 is the molar mass--that is, the mass of
is the molar mass--that is, the mass of
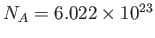 gas
molecules. Here,
gas
molecules. Here, 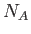 is Avogadro's number (Reif 1965).
is Avogadro's number (Reif 1965).
For all gases, whether in mean motion, or not, there exists an internal energy function, 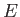 , that is
independent of the mean motion, and dependent only on the variables of state,
, that is
independent of the mean motion, and dependent only on the variables of state, 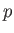 ,
, 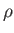 , and
, and 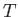 .
Moreover, this function is such that when a small quantity of heat,
.
Moreover, this function is such that when a small quantity of heat, 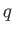 , is added to the
system (Reif 1965),
, is added to the
system (Reif 1965),
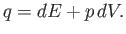 |
(14.2) |
Thus, the quantity 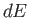 is the excess of the energy supplied over the mechanical work
done by the pressure. Of course, internal energy is an extensive quantity. The
corresponding intensive quantity is the specific internal energy,
is the excess of the energy supplied over the mechanical work
done by the pressure. Of course, internal energy is an extensive quantity. The
corresponding intensive quantity is the specific internal energy,
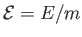 .
In an ideal gas, the specific internal energy,
.
In an ideal gas, the specific internal energy, 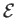 , is a function of the absolute
temperature,
, is a function of the absolute
temperature, 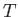 , alone (Reif 1965). It follows that
, alone (Reif 1965). It follows that
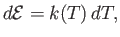 |
(14.3) |
and Equation (14.2) becomes
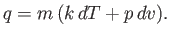 |
(14.4) |
The heat capacity at constant volume of the gas is defined
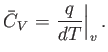 |
(14.5) |
Thus, Equation (14.4) implies that
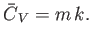 |
(14.6) |
It is clear that
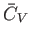 is an extensive quantity. The corresponding
intensive quantity is the specific heat capacity at constant volume,
is an extensive quantity. The corresponding
intensive quantity is the specific heat capacity at constant volume,
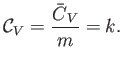 |
(14.7) |
Finally, the molar specific heat capacity at constant volume, which is the heat capacity of Avogadro's number
of gas molecules, takes the form
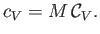 |
(14.8) |
It follows, from the preceding equations, that
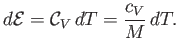 |
(14.9) |
In an ideal gas, 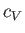 is a constant, independent of the temperature (Reif 1965), in which case the previous equation
can be integrated to give [cf., Equation (1.83)]
is a constant, independent of the temperature (Reif 1965), in which case the previous equation
can be integrated to give [cf., Equation (1.83)]
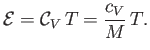 |
(14.10) |
Equation (14.1) yields
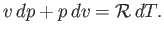 |
(14.11) |
Combining the previous equation with Equations (14.4) and (14.7), we obtain
![$\displaystyle q = m\left[({\cal C}_V+{\cal R})\,T-v\,dp\right].$](img5310.png) |
(14.12) |
Now, the heat capacity at constant pressure of the gas is defined
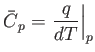 |
(14.13) |
Thus, Equation (14.12) implies that
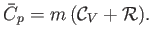 |
(14.14) |
It is clear that
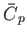 is an extensive quantity. The corresponding
intensive quantity is the specific heat capacity at constant pressure,
is an extensive quantity. The corresponding
intensive quantity is the specific heat capacity at constant pressure,
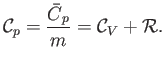 |
(14.15) |
Finally, the molar specific heat capacity at constant pressure, which is the heat capacity of Avogadro's number
of gas molecules, takes the form [cf., Equation (1.86)]
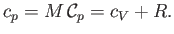 |
(14.16) |
The molar specific heat capacity at constant pressure of an ideal gas is a constant, independent of the
temperature.
The enthalpy of a gas is defined (Reif 1965)
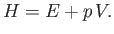 |
(14.17) |
This quantity is obviously extensive. The corresponding intensive quantity is the specific enthalpy,
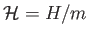 .
It follows that, for an ideal gas,
.
It follows that, for an ideal gas,
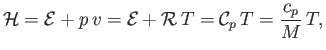 |
(14.18) |
where use has been made of Equations (14.1), (14.10), (14.15), and (14.16).
In the preceding analysis, we denoted a small quantity of heat by 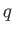 , rather than
, rather than 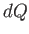 , because there is, in general,
no function
, because there is, in general,
no function 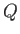 of which
of which 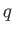 is an exact differential. However, we can write (Reif 1965)
is an exact differential. However, we can write (Reif 1965)
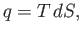 |
(14.19) |
where 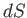 is the differential of an extensive function,
is the differential of an extensive function, 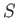 , called the entropy.
To justify the previous expression, note from Equations (14.1), (14.4) and (14.7) that
, called the entropy.
To justify the previous expression, note from Equations (14.1), (14.4) and (14.7) that
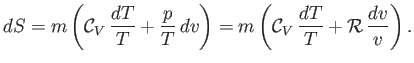 |
(14.20) |
However, Equation (14.1) yields
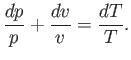 |
(14.21) |
Hence, we obtain
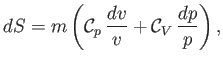 |
(14.22) |
where use has been made of Equation (14.15). In an ideal gas,
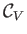 and
and
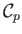 are constants, independent of
are constants, independent of 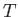 ,
so the previous expression can be integrated to give
,
so the previous expression can be integrated to give
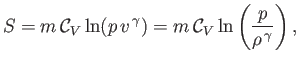 |
(14.23) |
where
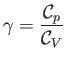 |
(14.24) |
is the constant ratio of specific heats. Obviously, the specific entropy is defined
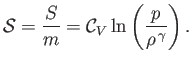 |
(14.25) |
Furthermore, it follows from Equations (14.2), (14.17), and (14.19) that
or, equivalently,



Next: Isentropic Flow
Up: One-Dimensional Compressible Inviscid Flow
Previous: Introduction
Richard Fitzpatrick
2016-03-31
![]() , that is
independent of the mean motion, and dependent only on the variables of state,
, that is
independent of the mean motion, and dependent only on the variables of state, ![]() ,
, ![]() , and
, and ![]() .
Moreover, this function is such that when a small quantity of heat,
.
Moreover, this function is such that when a small quantity of heat, ![]() , is added to the
system (Reif 1965),
, is added to the
system (Reif 1965),
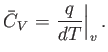
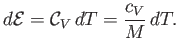
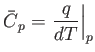
![]() , rather than
, rather than ![]() , because there is, in general,
no function
, because there is, in general,
no function ![]() of which
of which ![]() is an exact differential. However, we can write (Reif 1965)
is an exact differential. However, we can write (Reif 1965)