Next: Wave Optics Up: Dispersive Waves Previous: Capillary Waves Contents
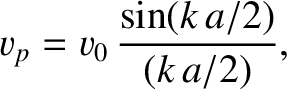
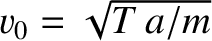 ,
,  is the tension in the string,
is the tension in the string,  the
spacing between the beads,
the
spacing between the beads,  the mass of the beads, and
the mass of the beads, and  the wavenumber
of the wave. What is the group velocity?
the wavenumber
of the wave. What is the group velocity?
 and length
and length  hangs vertically.
Determine the tension
hangs vertically.
Determine the tension  in the rope as a function of height from the bottom
of the rope. Show that the time required for a transverse wave pulse to
travel from the bottom to the top of the rope is
in the rope as a function of height from the bottom
of the rope. Show that the time required for a transverse wave pulse to
travel from the bottom to the top of the rope is
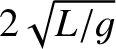 .
.
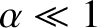 .
.
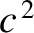 at all wave
frequencies, where
at all wave
frequencies, where 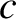 is the velocity of light in vacuum. Demonstrate that the dispersion relation for
electromagnetic waves takes the form
is the velocity of light in vacuum. Demonstrate that the dispersion relation for
electromagnetic waves takes the form
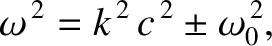
 is a constant.
is a constant.
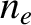 , as a
function of vertical height,
, as a
function of vertical height,  , is measured by timing how long it takes a radio pulse
launched vertically upward from the ground (
, is measured by timing how long it takes a radio pulse
launched vertically upward from the ground ( ) to return to ground level again, after
reflection by the ionosphere, as a function of the pulse frequency,
) to return to ground level again, after
reflection by the ionosphere, as a function of the pulse frequency,  .
It is conventional to define the equivalent height,
.
It is conventional to define the equivalent height, 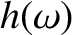 , of the reflection layer
as the height it would need to have above the ground if the pulse always traveled
at the velocity of light in vacuum. Demonstrate that
, of the reflection layer
as the height it would need to have above the ground if the pulse always traveled
at the velocity of light in vacuum. Demonstrate that
![$\displaystyle h(\omega) = \int_0^{z_0}\frac{dz}{[1-\omega_{p\,e}^{\,2}(z)/\omega^{\,2}]^{1/2}},
$](img3181.png)
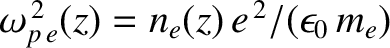 , and
, and
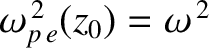 . Show that if
. Show that if
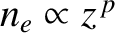 then
then
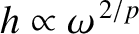 .
.
 |
 |
|
 |
 |
|
 |
 |
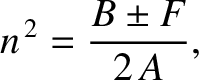
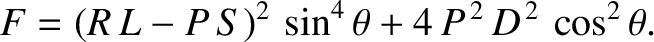
 is always real, and that
is always real, and that  is either purely real,
or purely imaginary. This implies that electromagnetic waves in (cold)
magnetized plasmas either propagate without evanescence, or decay without spatial
oscillation.
is either purely real,
or purely imaginary. This implies that electromagnetic waves in (cold)
magnetized plasmas either propagate without evanescence, or decay without spatial
oscillation.
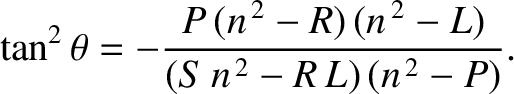
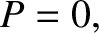
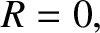
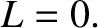
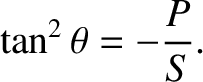
 -direction
through a conducting medium of conductivity
-direction
through a conducting medium of conductivity  . Suppose that the
wave electric field is
. Suppose that the
wave electric field is

 is the skin-depth. Demonstrate that the mean electromagnetic energy
flux across the plane
is the skin-depth. Demonstrate that the mean electromagnetic energy
flux across the plane 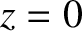 matches the mean rate at which electromagnetic
energy is dissipated, per unit area, due to Joule heating in the region
matches the mean rate at which electromagnetic
energy is dissipated, per unit area, due to Joule heating in the region 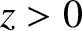 . [The rate
of Joule heating per unit volume is
. [The rate
of Joule heating per unit volume is
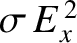 (Fitzpatrick 2008).]
(Fitzpatrick 2008).]
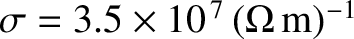 ,
and a typical thickness
,
and a typical thickness
 (Wikipedia contributors 2018). Show that such foil can be used to shield a region from electromagnetic
waves of a given frequency, provided that the skin-depth of the waves in the foil is less than about a third of its thickness.
Because skin-depth increases as frequency decreases, it follows that the foil can only shield waves whose frequency exceeds a critical
value.
Estimate this critical frequency (in hertz). What is the corresponding wavelength?
(Wikipedia contributors 2018). Show that such foil can be used to shield a region from electromagnetic
waves of a given frequency, provided that the skin-depth of the waves in the foil is less than about a third of its thickness.
Because skin-depth increases as frequency decreases, it follows that the foil can only shield waves whose frequency exceeds a critical
value.
Estimate this critical frequency (in hertz). What is the corresponding wavelength?
 -axis, and has perfectly conducting walls located at
-axis, and has perfectly conducting walls located at 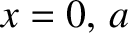 and
and 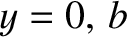 .
Maxwell's equations for a TE mode (which is characterized by
.
Maxwell's equations for a TE mode (which is characterized by 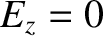 ) are (see Appendix C)
) are (see Appendix C)
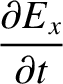 |
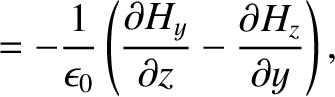 |
|
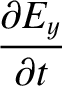 |
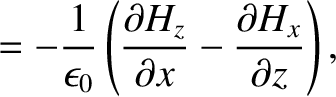 |
|
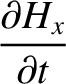 |
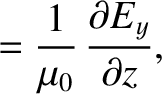 |
|
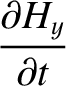 |
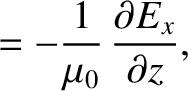 |
|
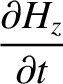 |
 |
 at
at 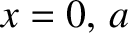 and
and 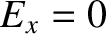 at
at 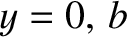 . Show that the problem reduces to
solving
. Show that the problem reduces to
solving
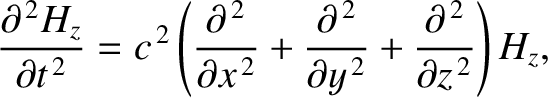
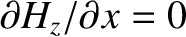 at
at 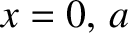 , and
, and
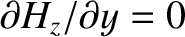 at
at 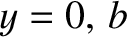 . Demonstrate that
the various TE modes satisfy the dispersion relation
. Demonstrate that
the various TE modes satisfy the dispersion relation

 is the
is the  -component of the wavevector,
-component of the wavevector,

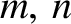 are non-negative integers, one of which must be non-zero.
are non-negative integers, one of which must be non-zero.
 -axis, and has perfectly conducting walls located at
-axis, and has perfectly conducting walls located at 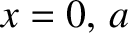 and
and 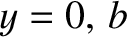 .
Maxwell's equations for a TM mode (which is characterized by
.
Maxwell's equations for a TM mode (which is characterized by 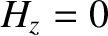 ) are (see Appendix C)
) are (see Appendix C)
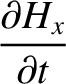 |
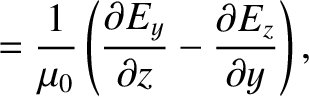 |
|
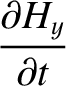 |
 |
|
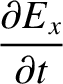 |
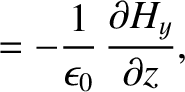 |
|
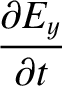 |
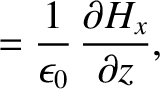 |
|
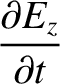 |
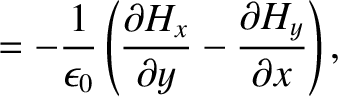 |
 at
at 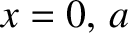 ,
, 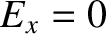 at
at 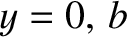 , and
, and 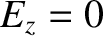 at
at 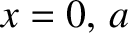 and
and 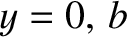 . Show that the problem reduces to
solving
. Show that the problem reduces to
solving
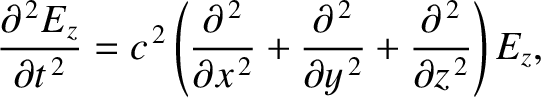
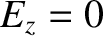 at
at 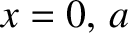 and
and 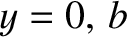 . Demonstrate that
the various TM modes satisfy the dispersion relation
. Demonstrate that
the various TM modes satisfy the dispersion relation

 is the
is the  -component of the wavevector,
-component of the wavevector,

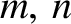 are positive integers.
are positive integers.
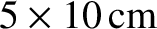 . What is the frequency
(in MHz) of the lowest frequency TE mode that will propagate along the waveguide without attenuation?
What are the phase and group velocities (expressed as multiples of
. What is the frequency
(in MHz) of the lowest frequency TE mode that will propagate along the waveguide without attenuation?
What are the phase and group velocities (expressed as multiples of 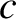 ) of this mode when its
frequency is
) of this mode when its
frequency is 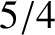 times the cutoff frequency?
times the cutoff frequency?
 -
- plane through an inhomogeneous medium with the
linear dispersion relation
plane through an inhomogeneous medium with the
linear dispersion relation
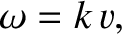

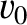 and
and  are positive constants.
Show that if
are positive constants.
Show that if 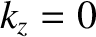 at
at 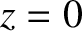 then the equations of motion of the pulse can be written
then the equations of motion of the pulse can be written
 |
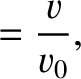 |
|
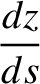 |
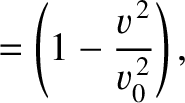 |
|
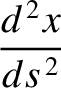 |
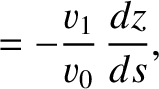 |
|
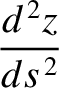 |
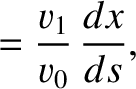 |
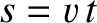 denotes path-length. Hence, deduce that the pulse travels in the arc of a circle, of radius
denotes path-length. Hence, deduce that the pulse travels in the arc of a circle, of radius
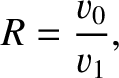
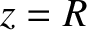 .
.
 , above the Earth's surface as
, above the Earth's surface as

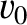 and
and  are positive constants, show that sound generated by a source located a height
are positive constants, show that sound generated by a source located a height
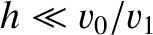 above the
ground is refracted upward by the atmosphere such that it never reaches ground level at points whose radial distances from the
point lying directly beneath the source exceed the value
above the
ground is refracted upward by the atmosphere such that it never reaches ground level at points whose radial distances from the
point lying directly beneath the source exceed the value
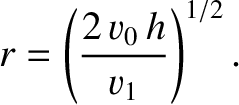
 toward the shore. Assuming that the
wave travels at right-angles to the shoreline, show that its wavelength and vertical amplitude vary as
toward the shore. Assuming that the
wave travels at right-angles to the shoreline, show that its wavelength and vertical amplitude vary as
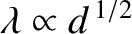 and
and
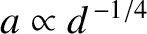 , respectively.
, respectively.
 and wavenumber
and wavenumber  , traveling over the surface of a lake of uniform depth
, traveling over the surface of a lake of uniform depth  causes an individual water volume element located at a depth
causes an individual water volume element located at a depth 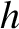 below the surface to execute a non-propagating elliptical orbit
whose major and minor axes are horizontal and vertical, respectively. Show that
the variation of the major and minor radii of the orbit with depth is
below the surface to execute a non-propagating elliptical orbit
whose major and minor axes are horizontal and vertical, respectively. Show that
the variation of the major and minor radii of the orbit with depth is
![$A\,\cosh[k\,(d-h)]$](img3243.png) and
and
![$A\,\sinh[k\,(d-h)]$](img3244.png) , respectively, where
, respectively, where 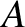 is a constant. Demonstrate that
the volume elements are moving horizontally in the same direction as the wave
at the top of their orbits, and in the opposite direction at the bottom.
Show that a gravity wave traveling over the surface of a very deep lake causes water volume elements to execute
non-propagating circular orbits whose radii decrease exponentially with depth.
is a constant. Demonstrate that
the volume elements are moving horizontally in the same direction as the wave
at the top of their orbits, and in the opposite direction at the bottom.
Show that a gravity wave traveling over the surface of a very deep lake causes water volume elements to execute
non-propagating circular orbits whose radii decrease exponentially with depth.
 and breadth
and breadth  to a depth
to a depth  .
Show that the resonant frequencies of the water are
.
Show that the resonant frequencies of the water are
![$\displaystyle \omega_{m,n}=\left[g\,k_{m,n}\,\tanh(k_{m,n}\,d)\right]^{1/2}
$](img3245.png)

 ,
,  are non-negative integers that are not both zero. Neglect surface tension.
are non-negative integers that are not both zero. Neglect surface tension.

 the phase velocity of surface waves can only attain a stationary (i.e., maximum or minimum) value
as a function of wavenumber,
the phase velocity of surface waves can only attain a stationary (i.e., maximum or minimum) value
as a function of wavenumber,  , when
, when
![$\displaystyle k = \left[\frac{\sinh(2\,k\,d)-2\,k\,d}{\sinh(2\,k\,d)+2\,k\,d}\right]^{1/2} k_c,
$](img3248.png)
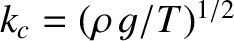 . Hence, deduce that the phase velocity has just one stationary value (a minimum) for any
depth greater than
. Hence, deduce that the phase velocity has just one stationary value (a minimum) for any
depth greater than
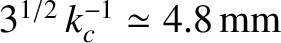 , but no stationary values for lesser depths.
, but no stationary values for lesser depths.
 times their phase velocities. Adapt the analysis of
Section 9.14 to investigate the generation of capillary waves by a very small object traveling across the surface of the water at
the constant speed
times their phase velocities. Adapt the analysis of
Section 9.14 to investigate the generation of capillary waves by a very small object traveling across the surface of the water at
the constant speed 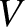 . Suppose that the unperturbed surface corresponds to the
. Suppose that the unperturbed surface corresponds to the  -
- plane.
Let the object travel in the minus
plane.
Let the object travel in the minus  -direction, such that it is instantaneously found at the origin. Find the present
position of waves that were emitted with wavefronts traveling at an angle
-direction, such that it is instantaneously found at the origin. Find the present
position of waves that were emitted with wavefronts traveling at an angle  to the object's direction of motion (see Figure 9.6), when it was located at
to the object's direction of motion (see Figure 9.6), when it was located at 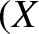 ,
, 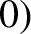 .
Show that along a given interference maximum the quantities
.
Show that along a given interference maximum the quantities 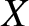 and
and  vary in such a manner that
vary in such a manner that
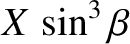 takes a constant value,
takes a constant value, 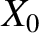 (say). Deduce that the interference maximum is given parametrically by the equations
(say). Deduce that the interference maximum is given parametrically by the equations
 |
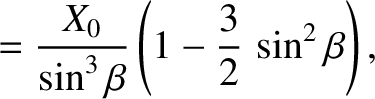 |
|
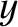 |
 |