Electromagnetic Theory
The subset of Maxwell's equations that governs the propagation of electromagnetic waves can be written
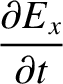 |
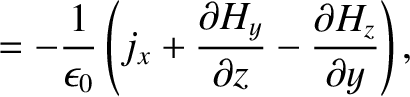 |
(C.1) |
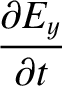 |
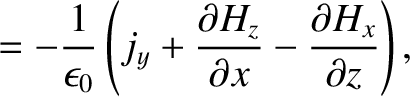 |
(C.2) |
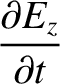 |
 |
(C.3) |
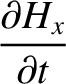 |
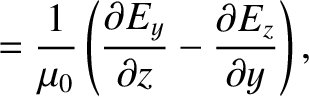 |
(C.4) |
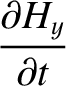 |
 |
(C.5) |
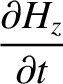 |
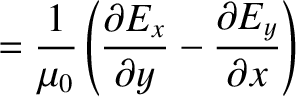 |
(C.6) |
 is the electric field-strength,
is the electric field-strength,  the magnetic intensity,
the magnetic intensity,  the current density (i.e., the current per
unit area),
the current density (i.e., the current per
unit area),
 the electric permittivity of free space, and
the electric permittivity of free space, and  the magnetic permeability of free space.
the magnetic permeability of free space.
For the case of a vacuum,
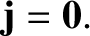 |
(C.7) |
Hence, the previous equations simplify to give
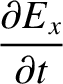 |
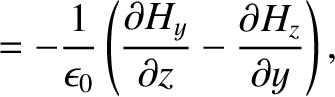 |
(C.8) |
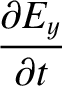 |
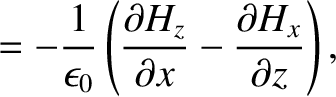 |
(C.9) |
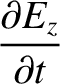 |
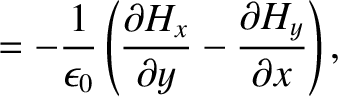 |
(C.10) |
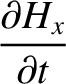 |
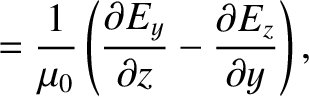 |
(C.11) |
For the case of a dielectric medium,
 |
(C.14) |
where 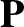 is the electric dipole moment per unit volume (Fitzpatrick 2008). Hence, we obtain
Now, the electric displacement is defined
is the electric dipole moment per unit volume (Fitzpatrick 2008). Hence, we obtain
Now, the electric displacement is defined
 |
(C.21) |
Moreover, in a linear dielectric medium,
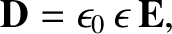 |
(C.22) |
where 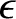 is the relative dielectric constant (Fitzpatrick 2008).
Thus, we get
is the relative dielectric constant (Fitzpatrick 2008).
Thus, we get
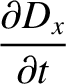 |
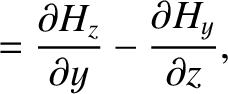 |
(C.23) |
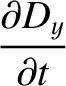 |
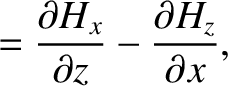 |
(C.24) |
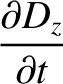 |
 |
(C.25) |
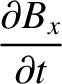 |
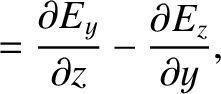 |
(C.26) |
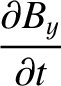 |
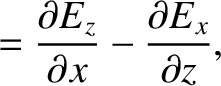 |
(C.27) |
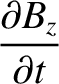 |
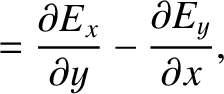 |
(C.28) |
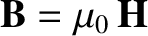 is the magnetic field-strength.
The previous three equations can also be written
where
is the magnetic field-strength.
The previous three equations can also be written
where
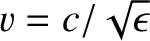 is the characteristic wave speed, and
is the characteristic wave speed, and
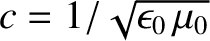 the
speed of light in vacuum.
the
speed of light in vacuum.
In an Ohmic conductor,
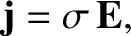 |
(C.32) |
where 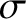 is the electrical conductivity (Fitzpatrick 2008). Thus, the equations governing
electromagnetic wave propagation in such a
medium become
is the electrical conductivity (Fitzpatrick 2008). Thus, the equations governing
electromagnetic wave propagation in such a
medium become
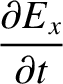 |
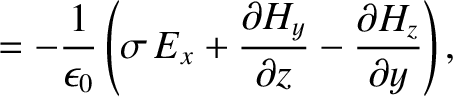 |
(C.33) |
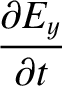 |
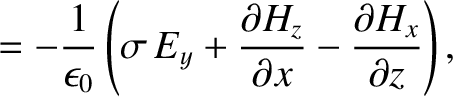 |
(C.34) |
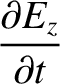 |
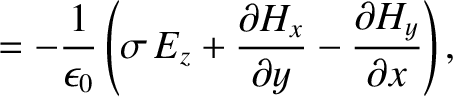 |
(C.35) |
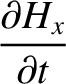 |
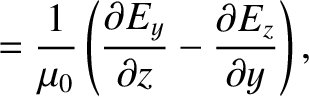 |
(C.36) |
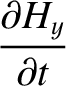 |
 |
(C.37) |
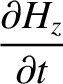 |
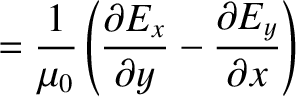 |
(C.38) |
The energy flux associated with an electromagnetic wave has the components
irrespective of the medium (Fitzpatrick 2008).
If 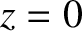 is the interface between two different (non-magnetic) media then the general matching conditions
for the components of the electric and magnetic fields across the interface are
is the interface between two different (non-magnetic) media then the general matching conditions
for the components of the electric and magnetic fields across the interface are
![$\displaystyle [E_x]_{z=0_-}^{z=0_+}$](img4464.png) |
 |
(C.42) |
![$\displaystyle [E_y]_{z=0_-}^{z=0_+}$](img4465.png) |
 |
(C.43) |
![$\displaystyle [D_z]_{z=0_-}^{z=0_+}$](img4466.png) |
 |
(C.44) |
![$\displaystyle [H_x]_{z=0_-}^{z=0_+}$](img4467.png) |
 |
(C.45) |
![$\displaystyle [H_y]_{z=0_-}^{z=0_+}$](img4468.png) |
 |
(C.46) |
![$\displaystyle [H_z]_{z=0_-}^{z=0_+}$](img4469.png) |
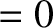 |
(C.47) |
The equation of motion of a particle of mass  and charge
and charge 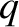 situated in electric and magnetic fields is
situated in electric and magnetic fields is
where
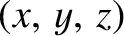 are the particle's Cartesian coordinates, and
are the particle's Cartesian coordinates, and
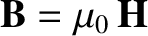 is the magnetic field-strength (Fitzpatrick 2008).
is the magnetic field-strength (Fitzpatrick 2008).
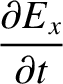
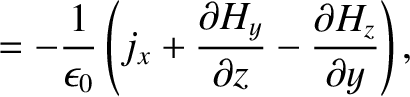
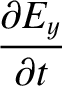
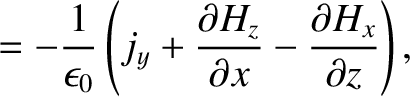
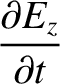

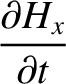
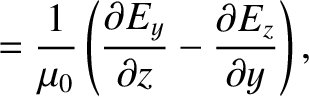
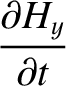

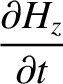
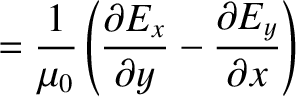
 is the electric field-strength,
is the electric field-strength,  the magnetic intensity,
the magnetic intensity,  the current density (i.e., the current per
unit area),
the current density (i.e., the current per
unit area),
 the electric permittivity of free space, and
the electric permittivity of free space, and  the magnetic permeability of free space.
the magnetic permeability of free space.
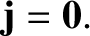
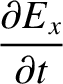
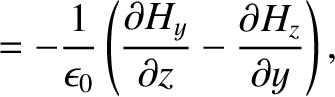
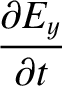
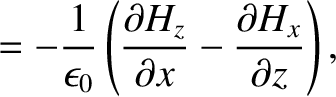
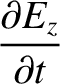
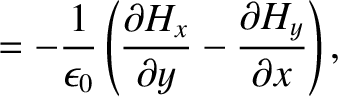
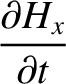
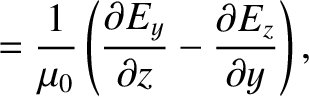
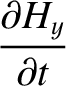

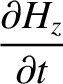
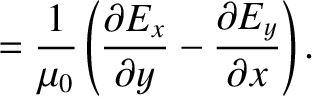

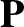 is the electric dipole moment per unit volume (Fitzpatrick 2008). Hence, we obtain
Now, the electric displacement is defined
is the electric dipole moment per unit volume (Fitzpatrick 2008). Hence, we obtain
Now, the electric displacement is defined

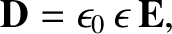
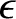 is the relative dielectric constant (Fitzpatrick 2008).
Thus, we get
is the relative dielectric constant (Fitzpatrick 2008).
Thus, we get
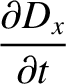
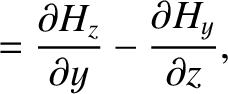
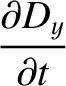
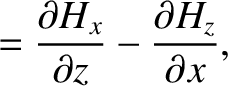
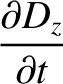

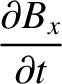
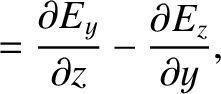
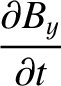
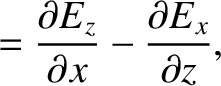
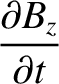
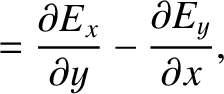
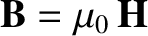 is the magnetic field-strength.
The previous three equations can also be written
is the magnetic field-strength.
The previous three equations can also be written
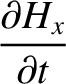
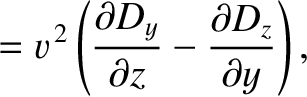
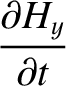

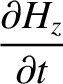
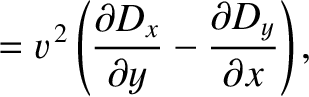
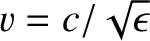 is the characteristic wave speed, and
is the characteristic wave speed, and
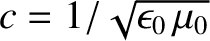 the
speed of light in vacuum.
the
speed of light in vacuum.
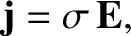
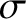 is the electrical conductivity (Fitzpatrick 2008). Thus, the equations governing
electromagnetic wave propagation in such a
medium become
is the electrical conductivity (Fitzpatrick 2008). Thus, the equations governing
electromagnetic wave propagation in such a
medium become
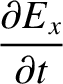
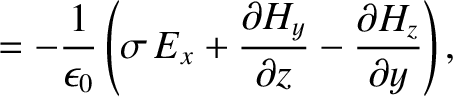
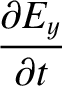
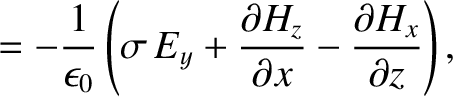
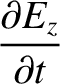
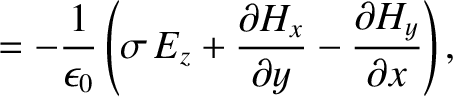
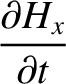
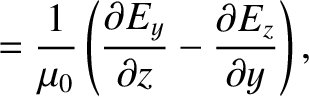
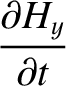

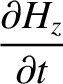
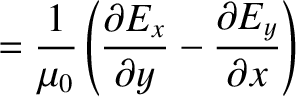
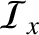
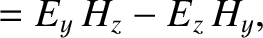
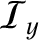
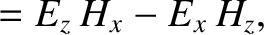
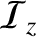
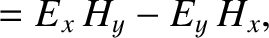
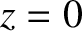 is the interface between two different (non-magnetic) media then the general matching conditions
for the components of the electric and magnetic fields across the interface are
is the interface between two different (non-magnetic) media then the general matching conditions
for the components of the electric and magnetic fields across the interface are
![$\displaystyle [E_x]_{z=0_-}^{z=0_+}$](img4464.png)

![$\displaystyle [E_y]_{z=0_-}^{z=0_+}$](img4465.png)

![$\displaystyle [D_z]_{z=0_-}^{z=0_+}$](img4466.png)

![$\displaystyle [H_x]_{z=0_-}^{z=0_+}$](img4467.png)

![$\displaystyle [H_y]_{z=0_-}^{z=0_+}$](img4468.png)

![$\displaystyle [H_z]_{z=0_-}^{z=0_+}$](img4469.png)
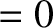
 and charge
and charge 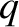 situated in electric and magnetic fields is
situated in electric and magnetic fields is

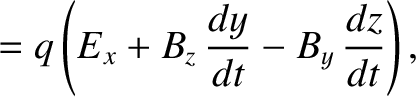

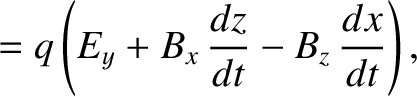
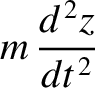
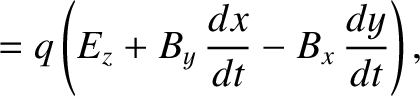
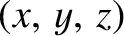 are the particle's Cartesian coordinates, and
are the particle's Cartesian coordinates, and
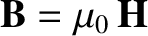 is the magnetic field-strength (Fitzpatrick 2008).
is the magnetic field-strength (Fitzpatrick 2008).