Next: Capillary Waves Up: Dispersive Waves Previous: Wave Drag on Ships Contents
 -
- plane. The
ship is traveling along the
plane. The
ship is traveling along the  -axis, in the negative
-axis, in the negative  -direction, at the constant speed
-direction, at the constant speed 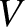 . Suppose that the ship's bow is initially at point
. Suppose that the ship's bow is initially at point 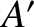 ,
and has moved to point
,
and has moved to point 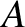 after a time interval
after a time interval  . The only type of gravity wave that is continuously excited by the passage of the ship
is one that maintains a constant phase relation with respect to its bow. In fact, as we have already mentioned, the bow should always correspond to a wave maximum.
An oblique wavefront associated with such a wave is shown in the figure. Here, the wavefront
. The only type of gravity wave that is continuously excited by the passage of the ship
is one that maintains a constant phase relation with respect to its bow. In fact, as we have already mentioned, the bow should always correspond to a wave maximum.
An oblique wavefront associated with such a wave is shown in the figure. Here, the wavefront 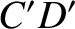 , which initially passes through the bow at point
, which initially passes through the bow at point 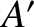 , has moved
to
, has moved
to 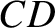 after a time interval
after a time interval  , such that it again passes through the bow at point
, such that it again passes through the bow at point 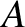 . The wavefront propagates at the
phase velocity,
. The wavefront propagates at the
phase velocity, 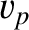 . It follows that, in the right-angled triangle
. It follows that, in the right-angled triangle  , the sides
, the sides 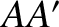 and
and  are of lengths
are of lengths  and
and  , respectively,
so that
This, therefore, is the condition that must be satisfied in order for an obliquely propagating gravity wave to maintain a constant phase relation with respect to the ship.
, respectively,
so that
This, therefore, is the condition that must be satisfied in order for an obliquely propagating gravity wave to maintain a constant phase relation with respect to the ship.
In shallow water, all gravity waves propagate at the same phase velocity. That is,
 |
(9.309) |
 is the water depth. Hence, Equation (9.308) yields
This equation can only be satisfied when
is the water depth. Hence, Equation (9.308) yields
This equation can only be satisfied when
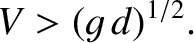 |
(9.311) |
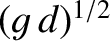 .
Moreover, if this is the case then there is only one value of
.
Moreover, if this is the case then there is only one value of  that satisfies Equation (9.310). This implies the scenario illustrated in
Figure 9.7. Here, the ship is instantaneously at
that satisfies Equation (9.310). This implies the scenario illustrated in
Figure 9.7. Here, the ship is instantaneously at 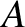 , and the wave maxima that it previously generated—which all
propagate obliquely, subtending a fixed angle
, and the wave maxima that it previously generated—which all
propagate obliquely, subtending a fixed angle  with the
with the  -axis—have interfered constructively
to produce a single strong wave maximum
-axis—have interfered constructively
to produce a single strong wave maximum 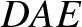 . In fact, the wave maxima generated when the ship was at
. In fact, the wave maxima generated when the ship was at 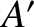 have travelled to
have travelled to
 and
and  , the wave maxima generated when the ship was at
, the wave maxima generated when the ship was at 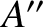 have travelled to
have travelled to  and
and 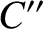 , et cetera. We conclude
that a ship traveling over shallow water produces a V-shaped wake whose semi-angle,
, et cetera. We conclude
that a ship traveling over shallow water produces a V-shaped wake whose semi-angle,  , is determined by the ship's speed.
Indeed, as is apparent from Equation (9.310), the faster the ship travels over the water, the smaller the angle
, is determined by the ship's speed.
Indeed, as is apparent from Equation (9.310), the faster the ship travels over the water, the smaller the angle  becomes.
Shallow water wakes are especially dangerous to other vessels, and particularly destructive of the coastline, because all
of the wave energy produced by the ship is concentrated into a single large wave maximum. The wake
contains no transverse waves, because, as we have already mentioned, such waves cannot keep up with a ship
traveling faster than the critical speed
becomes.
Shallow water wakes are especially dangerous to other vessels, and particularly destructive of the coastline, because all
of the wave energy produced by the ship is concentrated into a single large wave maximum. The wake
contains no transverse waves, because, as we have already mentioned, such waves cannot keep up with a ship
traveling faster than the critical speed
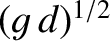 .
.
Let us now discuss the wake generated by a ship traveling over deep water. In this case, the phase velocity of
gravity waves is
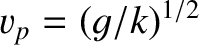 . Thus, Equation (9.308) yields
. Thus, Equation (9.308) yields
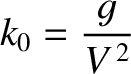 |
(9.313) |
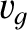 .
Furthermore, as we have already seen, the group velocity of deep water gravity waves is half their phase velocity; that is,
.
Furthermore, as we have already seen, the group velocity of deep water gravity waves is half their phase velocity; that is, 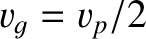 .
.
Consider Figure 9.8. The curve  corresponds to a particular interference maximum in the wake. Here,
corresponds to a particular interference maximum in the wake. Here,  is
the ship's instantaneous position. Consider a point
is
the ship's instantaneous position. Consider a point  on this curve. Let
on this curve. Let  and
and  be the coordinates of this point, relative to the
ship. The interference maximum at
be the coordinates of this point, relative to the
ship. The interference maximum at  is part of the plane wavefront
is part of the plane wavefront 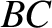 emitted some time
emitted some time  earlier, when the ship was at point
earlier, when the ship was at point 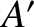 .
Let
.
Let  be the angle subtended between this wavefront and the
be the angle subtended between this wavefront and the  -axis.
Because interference maxima propagate at the group velocity, the distance
-axis.
Because interference maxima propagate at the group velocity, the distance 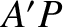 is equal to
is equal to 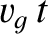 . The distance
. The distance 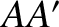 is
equal to
is
equal to  . Simple trigonometry reveals that
. Simple trigonometry reveals that
 |
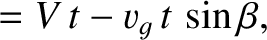 |
(9.314) |
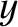 |
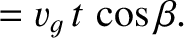 |
(9.315) |
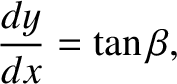 |
(9.316) |
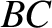 is the tangent to the curve
is the tangent to the curve  —that is, the curve
—that is, the curve 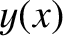 —at point
—at point 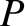 . It follows from Equation (9.312), and the fact that
. It follows from Equation (9.312), and the fact that 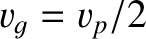 , that
, that
 |
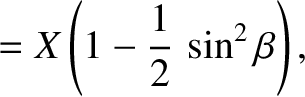 |
(9.317) |
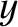 |
 |
(9.318) |
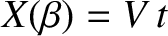 . The previous three equations can be combined to produce
. The previous three equations can be combined to produce
![$\displaystyle \frac{dy}{dx}=\frac{dy/d\beta}{dx/d\beta} = \frac{(1/2)\,dX/d\bet...
...\,[1-(1/2)\,\sin^2\beta]-X\,\sin\beta\,\cos\beta}
=\frac{\sin\beta}{\cos\beta},$](img3137.png) |
(9.319) |
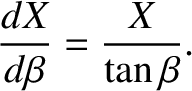 |
(9.320) |
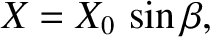 |
(9.321) |
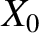 is a constant. Hence, the locus of our interference maximum is determined parametrically by
is a constant. Hence, the locus of our interference maximum is determined parametrically by
 |
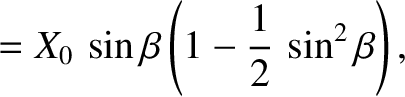 |
(9.322) |
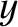 |
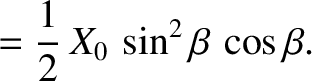 |
(9.323) |
 ranges
from
ranges
from  to
to  .
The curve specified by the previous equations is plotted in Figure 9.9. As usual,
.
The curve specified by the previous equations is plotted in Figure 9.9. As usual, 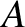 is the instantaneous
position of the ship. It can be seen that the interference maximum essentially consists of the transverse maximum
is the instantaneous
position of the ship. It can be seen that the interference maximum essentially consists of the transverse maximum  , and the two radial maxima
, and the two radial maxima 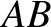 and
and 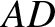 . As is readily demonstrated, point
. As is readily demonstrated, point  , which corresponds to
, which corresponds to
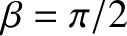 , lies at
, lies at 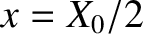 ,
, 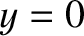 . Moreover, the
two cusps,
. Moreover, the
two cusps, 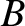 and
and 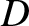 , which correspond to
, which correspond to
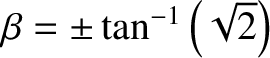 , lie at
, lie at
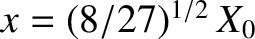 ,
,
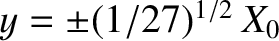 .
.
The complete interference pattern that constitutes the wake is constructed out of many different wave maximum curves of the form shown in Figure 9.9, corresponding to
many different values of the parameter 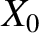 . However, these
. However, these 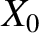 values must be chosen such that the wavelength of the pattern
along the
values must be chosen such that the wavelength of the pattern
along the  -axis corresponds to the wavelength
-axis corresponds to the wavelength
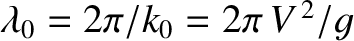 of transverse (i.e.,
of transverse (i.e.,
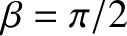 ) gravity waves whose
phase velocity matches the speed of the ship. This implies that
) gravity waves whose
phase velocity matches the speed of the ship. This implies that
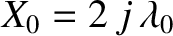 , where
, where  is a positive integer. A complete deep water wake pattern is
shown in Figure 9.10. The pattern, which is made up of interlocking transverse and radial wave maxima, fills a wedge-shaped region—known
as a Kelvin wedge—whose semi-angle takes the value
is a positive integer. A complete deep water wake pattern is
shown in Figure 9.10. The pattern, which is made up of interlocking transverse and radial wave maxima, fills a wedge-shaped region—known
as a Kelvin wedge—whose semi-angle takes the value
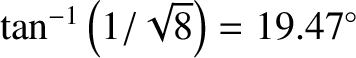 . This angle is independent of the ship's speed. Finally, our initial assumption that the gravity waves that form
the wake are all deep water waves is valid provided
. This angle is independent of the ship's speed. Finally, our initial assumption that the gravity waves that form
the wake are all deep water waves is valid provided
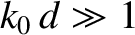 , which implies that
, which implies that
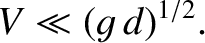 |
(9.324) |
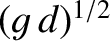 . This explains why the
wake contains transverse wave maxima.
. This explains why the
wake contains transverse wave maxima.